II.2.1 ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ

1. Импульс 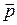(количество движения) материальной точки:

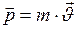(II.28)

Второй закон Ньютона (основное уравнение динамики материальной точки):

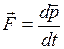(II.29)

Если масса постоянна, то второй закон Ньютона может быть выражен формулой:

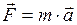, (II.30)

где - ускорение тела (материальной точки).

Если сила 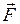постоянна по величине и действует по неизменному направлению, то изменение импульса тела за конечный промежуток времени равно произведению силы на время её действия:

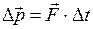или 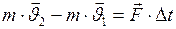, (II.31)

где 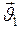и 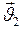- начальная и конечная скорости тела, разделённые промежутком времени .

Равенство (II.30) также выражает второй закон Ньютона. В случае переменной массы связь между силой, массой и ускорением выражается уравнением Мещерского:

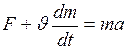, (II.32)

где 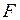- действующая сила; 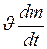- реактивная сила; 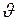- скорость присоединяющейся (отделяющейся) массы относительно тела.

2. Сила, действующая на материальную точку, движущуюся по криволинейной траектории, может быть разложена на две составляющие – тангенциальную и нормальную:

а) тангенциальная или касательная сила

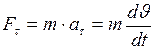, (II.33)

или

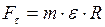, (II.34)

где 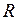- радиус кривизны траектории; 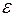- угловое ускорение.

б) нормальная или центростремительная сила:

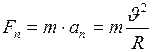, (II.35)

или

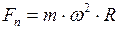, (II.36)

где 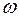- угловая скорость тела.

3. Центробежная сила инерции (в неинерциальной системе отсчёта):

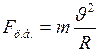, (II.37)

или

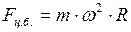. (II.38)

Центробежная сила инерции направлена вдоль радиус - вектора от центра или оси вращения.

4. Сила трения скольжения

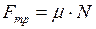, (II.39)

где 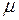- коэффициент трения скольжения; 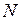- сила нормального давления.

5. Сила трения качения

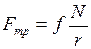, (II.40)

где 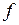- коэффициент трения качения; 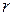- радиус катящегося тела.

6. Сила упругости

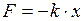, (II.41)

где 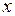- деформация тела; 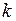- коэффициент жёсткости (упругости) тела.

7. Третий закон Ньютона

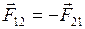, (II.42)

где 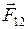и 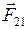- силы, с которыми взаимодействуют две материальные точки.

<29 30 313233 34 35 >

Дата добавления: 2016-09-06; просмотров: 2088;