Квадратурные формулы прямоугольников

На каждом частичном отрезке разбиения [x_k, x_{k + 1}], k = 0, 1, 2, …, n – 1воспользуемся квадратурной формулой вида

I_k » f(x_k)h, k = 0, 1, 2, …, n – 1. (4.3.9)

Тогда определенный интеграл от f(x) на всем отрезке [a, b] запишется в виде

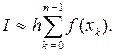(4.3.10)

Если на частичных отрезках воспользуемся квадратурной формулой

I_k » f(x_{k + 1})h, k = 0, 1, 2, …, n – 1, (4.3.11)

получим следующую составную квадратурную формулу для отрезка [a, b]:

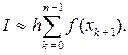(4.3.12)

Наконец, в качестве квадратурной формулы на частичных отрезках разбиения можно использовать формулу

I_k » f(x_{k + 1/2})h, k = 0, 1, 2, …, n – 1, (4.3.13)

где x_{k + ½} = (x_k + x_{k + 1})/2 – середина k-го отрезка разбиения [x_k, x_{k + 1}],
k = 0, 1, 2, …, n – 1.

В результате для отрезка [a, b] получим

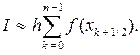(4.3.14)

Формулу (4.3.10) будем называть составной формулой левых прямоугольников, формулу (4.3.12) – составной формулой правых прямоугольников, формулу (4.3.14) см. ниже!!! – составной формулой центральных прямоугольников.

С геометрической точки зрения при использовании формул (4.3.9), (4.3.11) и (4.3.13) площадь под кривой y = f(x) заменяется на каждом частичном отрезке разбиения [x_k, x_{k + 1}] площадью прямоугольника шириной h и высотой, равной f(x_k), f(x_{k + 1}) или f(x_{k + 1/2}) соответственно, чем и объясняется название этих формул.

Для квадратурных формул (4.3.9) и (4.3.11) – левых и правых прямоугольников – справедлива следующая оценка погрешности аппроксимации:

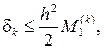(4.3.15)

где 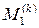– максимум модуля первой производной функции f(x) на k-м частичном отрезке разбиения [x_k, x_{k + 1}], k = 0, 1, 2, …, n – 1.

Для составных формул (4.3.10) и (4.3.12) оценка погрешности аппроксимации:

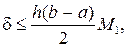(4.3.16)

где M₁ – максимум модуля первой производной функции f(x) на отрезке [a, b].

Для формулы центральных прямоугольников (4.3.13) см. выше!!! оценка погрешности аппроксимации

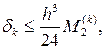(4.3.17)

где 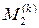– максимум модуля второй производной функции f(x) на k-м частичном отрезке разбиения [x_k, x_{k + 1}], k = 0, 1, 2, …, n – 1.

Для составной формулы центральных прямоугольников

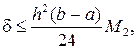(4.3.18)

где M₂ – максимум модуля второй производной функции f(x) на отрезке [a, b].

Считают, что формулы (4.3.10) и (4.3.12) имеют первый, формулы (4.3.9), (4.3.11) и (4.3.14) – второй, формула (4.3.13) – третий порядок точности по h.

Как следует из приведенных выше оценок погрешности аппроксимации, квадратурные формулы левых и правых прямоугольников точны для полиномов нулевого порядка, а квадратурная формула центральных прямоугольников – для полиномов до первого порядка включительно. Следует отметить, что вычисления с помощью квадратурной формулы центральных прямоугольников возможны, если значения f(x_{k + 1/2}), k = 0, 1, 2, …, n – 1 либо могут быть вычислены, либо уже заданы в имеющейся таблице значений функции.