Автоматический выбор шага. Правило Рунге
При выполнении практических расчетов с применением рассмотренных квадратурных формул оценку погрешности получаемых результатов можно осуществлять априорно, используя соотношения (4.3.15) – (4.3.18), (4.3.21), (4.3.22), (4.3.25) и (4.3.26). Эти соотношения позволяют получить (для заданного шага h между узлами равномерной сетки hx) оценку сверху для погрешности аппроксимации квадратурной формулы с точностью до максимума модуля производной того или иного порядка подынтегральной функции на отрезке интегрирования. С другой стороны, основываясь на этих соотношениях можно определить максимально возможное значение h, при котором удовлетворяются заданные требования к точности результатов расчета. Однако с практической точки зрения получить достоверную оценку максимума модуля производной, даже если известно аналитическое задание подынтегральной функции, достаточно сложно. Если аналитическое задание неизвестно (что чаще всего и имеет место), а функция представлена лишь табличными значениями, то задача получения такой оценки, как правило, становится практически неразрешимой. Таким образом, возникает необходимость применения других способов оценки погрешности численного интегрирования, один из которых основан на использовании правила Рунге.
В отличие от априорной (до того как будут произведены вычисления) оценки погрешности на основании соотношений (4.3.15) – (4.3.18), (4.3.21), (4.3.22), (4.3.25) и (4.3.26) для предлагаемого подхода имеет место апостериорная оценка, которая получается в результате анализа уже произведенных вычислений.
Пусть Ik – точное, а Jk(h) – приближенное значение определенного интеграла от функции f(x), полученное в результате расчета с шагом h по одной из рассмотренных ранее квадратурных формул на частичных отрезках разбиения [xk, xk + 1], k = 0, 1, 2, …, n – 1 отрезка [a, b]. Тогда будет справедливо приближенное равенство
Ik – Jk(h) » qkhm, k = 0, 1, 2, …, n – 1, (4.3.27)
где m – порядок точности используемой квадратурной формулы.
Напомним, что m = 2 для квадратурных формул левых (4.3.9) и правых (4.3.11) прямоугольников, m = 3 - для квадратурной формулы центральных (4.3.13) прямоугольников и квадратурной формулы (4.3.19) трапеций, m = 5 - для квадратурной формулы (4.3.23) Симпсона.
Уменьшим шаг сетки в два раза и повторим расчет по той же именно???? квадратурной формуле. Обозначим результат расчета как Jk(h/2). Для него справедливо аналогичное (4.3.27) приближенное равенство
Ik – Jk(h/2) » qk(h/2)m, k = 0, 1, 2, …, n – 1. (4.3.28)
Из соотношений (4.3.27) и (4.3.28) имеем
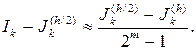 (4.3.29)
(4.3.29)
Полученное приближенное равенство часто называют правилом Рунге.
Пусть теперь задано достаточно малое число e > 0, определяющее требуемую точность вычисления значения определенного интеграла
от функции f(x) на отрезке [a, b] с помощью составной квадратурной формулы
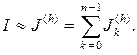 (4.3.30)
(4.3.30)
Здесь I – точное значение определенного интеграла на отрезке [a, b]; J(h) – приближенное значение этого интеграла, определенное с помощью составной квадратурной формулы.
Для каждого частичного отрезка разбиения [xk, xk + 1], k = 0, 1, 2, …, n – 1 дважды проведем вычисления по квадратурной формуле, имеющей порядок точности равный m, – с шагом h и h/2.
Согласно правилу Рунге (4.3.29) можно утверждать, что если
в результате для всех частичных отрезков разбиения будут выполняться неравенства
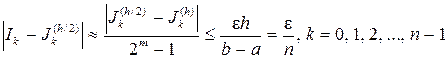 , (4.3.31)
, (4.3.31)
то очевидно, что для соответствующей составной квадратурной формулы требуемая точность будет обеспечена.
Если для некоторых частичных отрезков неравенство (4.3.31) не будет выполнено, то для них необходимо повторять расчет, уменьшая каждый раз шаг h сетки в два раза до тех пор, пока не будет обеспечено его выполнение.
Рассмотренная возможность выбора величины шага между узлами квадратурной формулы для обеспечения заданной точности вычисления лежит в основе процедур численного интегрирования с так называемым автоматическим выбором шага. Отметим, что такой способ определения шага позволяет в процессе численного интегрирования варьировать расстояние между узлами составной квадратурной формулы в области интегрирования. На участках, где интегрируемая функция f(x) медленно изменяет свои значения, шаг может оставаться достаточно большим, и лишь на участках наиболее быстрого изменения значений f(x) для обеспечения требуемой точности может потребоваться дробление шага.
Очевидно, что рассмотренная процедура автоматического выбора шага может быть реализована только в том случае, когда значения интегрируемой функции во вновь образующихся при дроблении шага узлах составной квадратурной формулы либо могут быть вычислены, либо уже заданы в имеющейся таблице ее значений.
Глава 5. Численные методы решения задачи Коши
для обыкновенных дифференциальных уравнений
и их систем
Основные понятия
В данном параграфе рассматриваются численные методы решения задачи Коши для обыкновенного дифференциального уравнения первого порядка и систем дифференциальных уравнений первого порядка.
Задача Коши для системы дифференциальных уравнений первого порядка формулируется следующим образом: найти функции yk = fk(x), k = 1, 2, …, n, удовлетворяющие системе дифференциальных уравнений
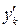 = gk(x, y1, y2, …, yn), k = 1, 2, …, n (5.1.1)
и начальным условиям
yk(x0) = y0(k), k = 1, 2, …, n, (5.1.2)
где y0(k), k = 1, 2, …, n – заданные числа. = gk(x, y1, y2, …, yn), k = 1, 2, …, n (5.1.1)
и начальным условиям
yk(x0) = y0(k), k = 1, 2, …, n, (5.1.2)
где y0(k), k = 1, 2, …, n – заданные числа.
|
Более подробно эту задачу можно сформулировать так: 
 найти функции yk = fk(x), k = 1, 2, …, n, удовлетворяющие системе дифференциальных уравнений
найти функции yk = fk(x), k = 1, 2, …, n, удовлетворяющие системе дифференциальных уравнений
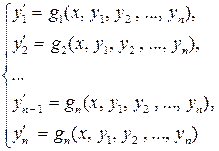 (5.1.3)
(5.1.3)
и начальным условиям
y1(x0) = y(1)0, y2(x0) = y(2)0, …, yn – 1(x0) = y(n – 1)0, yn(x0) = y(n)0, (5.1.4)
где y(1)0, y(2)0, …, y(n – 1)0, y(n)0 – заданные числа.
В дальнейшем предполагается, что условия теоремы существования и единственности для задачи (5.1.3), (5.1.4) выполнены.
Положим a:= x0 и будем искать решение задачи Коши (5.1.3), (5.1.4) на отрезке [a, b]. При построении численного решения получим приближенное решение задачи
j(1)h(x)»f1(x); j(2)h(x)»f2(x);…;j(n – 1)h(x)»fn – 1(x); j(n)h(x)»fn(x), (5.1.5)
которое представлено значениями функций j(k)h(x), k = 1, 2, …, n в узлах заданной на отрезке [a, b] одномерной сетки
hx = {xi/xi = xi – 1 + hi, hi > 0, i = 1, 2, 3, …, m; x0 = a, xm = b}, (5.1.6)
где xi, i = 0, 1, 2, …, m – узлы одномерной сетки; hi, i = 1, 2, 3, …, m – ее шаг.
Для простоты будем полагать, что сетка hx равномерная:
hi = h, i = 1, 2, 3, …, m. Таким образом, в результате численного решения задачи (5.1.3) - (5.1.4) получим значения j(k)h(x0), j(k)h(x1), j(k)h(x2), …, j(k)h(xn) функций j(k)h(x), k = 1, 2, …, n. Эти результаты удобно представлять в табличной форме (табл. 5.1.1).
Таблица 5.1.1
| Номер узла | Узлы сетки | j(1)h(x) » » f1(x) | j(2)h(x) » » f2(x) | j(3)h(x) » » f3(x) | … | j(n – 1)h(x) » » fn – 1(x) | j(n)h(x) » » fn(x) |
| x0 | j(1)h(x0) | j(2)h(x0) | j(3)h(x0) | … | j(n -- 1)h(x0) | j(n)h(x0) | |
| x1 | j(1)h(x1) | j(2)h(x1) | j(3)h(x1) | … | j(n -- 1)h(x1) | j(n)h(x1) | |
| x2 | j(1)h(x2) | j(2)h(x2) | j(3)h(x2) | … | j(n -- 1)h(x2) | j(n)h(x2) | |
| …. | … | … | … | … | ... | … | … |
| m – 1 | xm – 1 | j(1)h(xm – 1) | j(2)h(xm – 1) | j(3)h(xm -- 1) | … | j(n – 1)h(xm – 1) | j(n)h(xm – 1) |
| m | xm | j(1)h(xm) | j(2)h(xm) | j(3)h(xm) | … | j(n – 1)h(xm) | j(n)h(xm) |
Как известно, к задаче (5.1.3) - (5.1.4) сводится и задача Коши для обыкновенного дифференциального уравнения n-го порядка:

 найти функцию y = f(x), удовлетворяющую дифференциальному уравнению
найти функцию y = f(x), удовлетворяющую дифференциальному уравнению
y(n) = g(x, y, y¢, y(2), …, y(n – 2), y(n – 1)) (5.1.7)
и начальным условиям
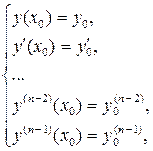 (5.1.8)
(5.1.8)
где 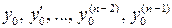 – заданные числа (здесь y(k) - производная k-го порядка функции y = f(x)).
– заданные числа (здесь y(k) - производная k-го порядка функции y = f(x)).
Сведение задачи (5.1.7) - (5.1.8) к решению системы дифференциальных уравнений вида (5.1.3), (5.1.4) осуществляется посредством переобозначения:
y1:= y¢; y2:= y(2);…; yn – 1:= y(n – 1); yn:= y(n). (5.1.9)
В результате вместо дифференциального уравнения n-го порядка (5.1.7) может быть записана система n дифференциальных уравнений первого порядка
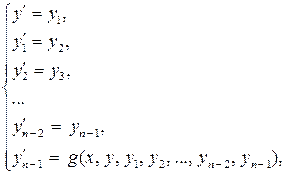 (5.1.10)
(5.1.10)
а начальные условия (5.1.8) переписываются в обозначениях (5.1.9), что приводит к задаче вида (5.1.3), (5.1.4).
 Как частный случай (n = 1) задачи (5.1.3), (5.1.4) запишем задачу Коши для дифференциального уравнения первого порядка, которая может быть сформулирована следующим образом:
Как частный случай (n = 1) задачи (5.1.3), (5.1.4) запишем задачу Коши для дифференциального уравнения первого порядка, которая может быть сформулирована следующим образом:


 найти функцию y = f(x), удовлетворяющую дифференциальному уравнению
найти функцию y = f(x), удовлетворяющую дифференциальному уравнению
y¢ = g(x, y) (5.1.11)
и начальному условию
y(x0) = y0, (5.1.12)
где y0 – заданное число.
Предположим, как и ранее, что условия теоремы существования
и единственности решения задачи (5.1.11), (5.1.12) выполнены. Положим a:= x0 и будем искать решение задачи Коши (5.1.11), (5.1.12) на отрез-
ке [a, b]. В результате численного решения поставленной задачи получим приближенное решение
jh(x) » f(x), (5.1.13)
которое представлено значениями jh(x) в узлах заданной на отрезке [a, b] одномерной равномерной сетки hx (5.1.6) с шагом h.
Таким образом, в результате численного решения задачи (5.1.11), (5.1.12) получаем значения jh(x0), jh(x1), jh(x2), …, jh(xm) функции jh(x) – приближенное решение задачи.
В последующих параграфах данной главы будут рассмотрены конкретные численные методы решения применительно к задаче (5.1.11), (5.1.12) – задаче Коши для одного обыкновенного дифференциального уравнения первого порядка. Вместе с тем рассматриваемые методы могут применяться и для решения задачи Коши для системы дифференциальных уравнений первого порядка (5.1.3), (5.1.4).
Рассматриваемые численные методы решения задачи Коши (5.1.11), (5.1.12) можно разделить на две группы:
– многошаговые разностные методы. К ним относятся метод Эйлера (§ 5.2) и явный 4-шаговый метод Адамса (§ 5.3);
– методы Рунге – Кутта (в § 5.4 будет рассмотрен метод Рунге – Кутта четвертого порядка).
Эти методы имеют некоторые общие свойства и характеристики.
Как следует из вышесказанного, jh(x) – приближенное решение, полученное в результате численного решения задачи Коши, представлено значениями в узлах одномерной равномерной сетки hx с шагом h - jh(x0), jh(x1),jh(x2), …, jh(xm). Расчет значений приближенного решения jh(x) в узлах сетки осуществляется для всех рассматриваемых численных методов решения задачи Коши по правилу
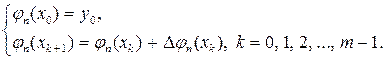 (5.1.14)
(5.1.14)
Таким образом, отличие одного численного метода от другого заключается лишь в способе построения Djh(xk), k = 0, 1, 2, …, m – 1.
Важными характеристиками численного метода являются также оценки погрешности и сходимость. Погрешность метода часто оценивают с помощью так называемого порядка точности метода.
Определение 5.1.1
| Численный метод решения задачи Коши (5.1.11) - (5.1.12) имеет порядок точности k > 0, если существует такое число q > 0, при котором выполнено условие ôjh(xm) – f(xm)ô£ qhk. (5.1.14) |
Определение 5.1.2
| Численный метод решения задачи Коши (5.1.11) - (5.1.12) сходится в точке xm = b, если выполнено условие lim (jh(xm) – f(xm)) = 0. (5.1.15) h ® 0 |
Следует отметить, что при стремлении шага h сетки к нулю общее количество узлов m равномерной сетки hx на отрезке [a, b] стремится к бесконечности.
Определение 5.1.3
| Численный метод решения задачи Коши (5.1.11) - (5.1.12) сходится на отрезке [a, b], если он сходится в каждой точке этого отрезка. |
Метод Эйлера
Пусть на отрезке [a, b] требуется найти решение задачи Коши для обыкновенного дифференциального уравнения первого порядка
y¢ = g(x, y), (5.2.1)
y(x0) = y0, (5.2.2)
где y0 – заданное число.
Зададим на отрезке [a, b] равномерную сетку
hx = {xi / xi = xi – 1 + h, h > 0, i = 1, 2, 3, …, m; x0 = a, xm = b}, (5.2.3)
где xi, i = 0, 1, 2, …, m – узлы одномерной сетки hx; h – шаг сетки.
 Приближенное решение jh(x) задачи (5.2.1) - (5.2.2) будем строить по правилу
Приближенное решение jh(x) задачи (5.2.1) - (5.2.2) будем строить по правилу
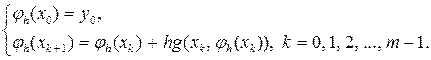 (5.2.4)
(5.2.4)
Организация вычислений при реализации метода Эйлера предельно проста. Промежуточные результаты удобно размещать в таблице, аналогичной табл. 5.2.1.
Таблица 5.2.1
| k | xk | jh(xk) = jh(xk – 1) + hg(xk – 1, jh(xk – 1)) | g(xk, jh(xk)) |
| x0 | jh(x0) (берется из начальных условий) | g(x0, jh(x0)) | |
| x1 | jh(x1) = jh(x0) + hg(x0,jh(x0)) | g(x1, jh(x1)) | |
| x2 | jh(x2) = jh(x1) + hg(x1, jh(x1)) | g(x2, jh(x2)) | |
| … | … | ||
| m – 1 | xm – 1 | jh(xm – 1) = jh(xm – 2) + hg(xm – 2, jh(xm – 2)) | g(xm – 1, jh(xm –- 1)) |
| m | xm | jh(xm) = jh(xm – 1) + hg(xm – 1, jh(xm – 1)) |
В заключение сделаем несколько замечаний относительно метода Эйлера (5.2.4).
1. Рассмотренный метод является явным одношаговым разностным. Это один из наиболее простых численных методов решения задачи Коши.
2. Сходится на отрезке [a, b] в соответствии с определением и имеет первый порядок точности.
3. Ввиду невысокой точности редко используется для решения реальных задач. Существуют модификации метода, позволяющие повысить точность получаемых результатов.
4. Легко адаптируется к решению задачи Коши для систем обыкновенных дифференциальных уравнений первого порядка.
Рассмотрим систему из двух уравнений
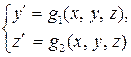
с начальными условиями
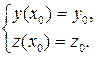
Как и ранее, будем искать решение поставленной задачи Коши на отрезке [a, b], задав на нем равномерную сетку hx с шагом h.
Пусть функции jh y(x) » y(x) и jh z(x) » z(x) обозначают приближенное решение задачи, тогда метод Эйлера запишется в виде
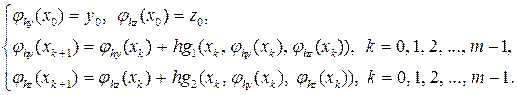
Дата добавления: 2021-07-22; просмотров: 1141;











