Явный 4-шаговый метод Адамса
Пусть на отрезке [a, b] требуется найти решение задачи Коши для обыкновенного дифференциального уравнения первого порядка
y¢ = g(x, y), (5.3.1)
y(x0) = y0, (5.3.2)
где y0 – заданное число.
Зададим на отрезке [a, b] равномерную сетку
hx = {xi / xi = xi – 1 + h, h > 0, i = 1, 2, 3, …, m; x0 = a, xm = b}, (5.3.3)
где xi, i = 0, 1, 2, …, m – узлы одномерной сетки hx; h – шаг сетки.
Введем обозначения
jh,k:=jh(xk); gk:=g(xk, jh(xk)). (5.3.4)
Явный 4-шаговый метод Адамса может быть представлен следующим образом. Положим jh(x0): = y0 и вычислим значение g0. Далее предположим, что значения g1, g2, g3 уже известны. Приближенное решение jh(x) задачи (5.3.1), (5.3.2) будем строить по правилу
jh, k + 1 = jh, k + (h/1224)[55gk – 59gk – 1 + 37gk – 2 – 9gk – 3],
k = 3, 4, …, m – 1. (5.3.5)
Отметим, что для определения g1, g2, g3 необходимо знать значения jh(x1), jh(x2), jh(x3), которые могут быть найдены предварительно с помощью любого другого численного метода либо заданы в результате каких-либо измерений.
Метод (5.3.5) называется 4-шаговым, поскольку для вычисления функции jh(xk) необходимо знать ее значения в четырех предыдущих узлах сетки hx.
Результаты вычислений методом (5.3.5) удобно записывать в таблицу, аналогичную табл. 5.3.1.
Таблица 5.3.1
| k | xk | jh, k = jh(xk – 1) + (h/1224)[55gk – 1 – 59gk – 2 + 37gk – 3 -9gk – 4] | gk = g(xk, jh(xk)) |
| x0 | jh, 0 = y0 берется из начальных условий | g0 = g(x0, jh(x0)) | |
| x1 | jh, 1 определяется другим методом | g1 = g(x1, jh(x1)) | |
| x2 | jh, 2 определяется другим методом | g2 = g(x2, jh(x2)) | |
| x3 | jh, 3 определяется другим методом | g3 = g(x3, jh(x3)) | |
| x4 | jh, 4 = jh(x3) + (h/1224)[55g3 – 59g2 + 37g1 – 9g0] | g4 = g(x4, jh(x4)) | |
| … | … | … | … |
| m – 1 | xm – 1 | jh, m – 1 = jh(xm – 2) + (h/1224)[55gm – 2 – 59gm – 3 + + 37gm – 4 – 9gm – 5] | gm – 1 = g(xm – 1, jh(xm – 1)) |
| m | xm | jh, m = jh(xm – 1) + (h/1224)[55gm – 1 – 59gm – 2 + + 37gm – 3 – 9gm – 4] |
В заключение сделаем несколько замечаний относительно метода Адамса.
1. Это явный 4-шаговый разностный метод, который, так же как и
метод Эйлера, является явным многошаговым. (Более подробное описание многошаговых разностных методов решения задачи Коши для обыкновенного дифференциального уравнения первого порядка приведено в литературе по вычислительной математике.)
2. Метод (5.3.5) является сходящимся на отрезке [a, b] в соответствии с определением и имеет четвертый порядок точности.
3. В отличие от одношагового метода Эйлера метод Адамса требует для начала работы предварительного определения значений искомой функции еще в трех узлах сетки hx, что является в определенном смысле его недостатком. На практике эта дополнительная информация может быть получена либо с помощью других численных методов (методов Эйлера, Рунге – Кутта), либо с помощью измерений иного характера.
4. Метод Адамса может быть легко адаптирован применительно
к решению задачи Коши для систем обыкновенных дифференциальных уравнений первого порядка.
Рассмотрим систему из двух уравнений
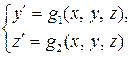
с начальными условиями
y(x0) = y0, z(x0) = z0.
Как и ранее, будем искать решение поставленной задачи Коши на отрезке [a, b], задав на нем равномерную сетку hx с шагом h.
Пусть функции jh, y(x) » y(x) и jh, z(x) » z(x) представляют собой приближенное решение задачи. Введем обозначения
jh, y,k:=jh,y(xk); g1,k:=g1(xk, jh,y(xk),jh,z(xk)),
jh, z,k:=jh,y,z(xk); g2, k:=g2(xk, jh, y(xk),jh,z(xk)).
Тогда метод Адамса перепишется в виде:

 Положивм jh, y(x0): = y0, jh, z(x0): = z0, вычислим значения g1, 0 и g2, 0.
Положивм jh, y(x0): = y0, jh, z(x0): = z0, вычислим значения g1, 0 и g2, 0.
Предположим, что уже известны значения g1, 1, g1, 2, g1, 3, g2, 1, g2, 2, g2, 3.
Значения jh, y(xk), jh, z(xk) "строим" по правилу:
 jh,y, k + 1 = jh,y,k + (h/24)[55g1,k – 59g1,k-1 + 37g1,k-2 – 9g1,k-3], k = 3,4,…, m-1
jh,y, k + 1 = jh,y,k + (h/24)[55g1,k – 59g1,k-1 + 37g1,k-2 – 9g1,k-3], k = 3,4,…, m-1
jh,z, k + 1 = jh,z,k + (h/24)[55g2,k – 59g2,k-1 + 37g2,k-2 – 9g2,k-3], k = 3,4,…, m-1
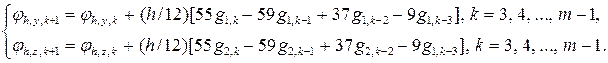
Дата добавления: 2021-07-22; просмотров: 721;











