Метод Рунге - Кутта четвертого порядка

Пусть на отрезке [a, b] требуется найти решение задачи Коши для обыкновенного дифференциального уравнения первого порядка

y¢ = g(x, y), (5.4.1)

y(x₀) = y₀, (5.4.2)

где y₀ – заданное число.

Зададим на отрезке [a, b] равномерную сетку

h_x = {x_i / x_i = x_{i – 1} + h, h > 0, i = 1, 2, 3, …, m; x₀ = a, x_m = b}, (5.4.3)

где x_i, i = 0, 1, 2, …, m – узлы одномерной сетки; h – шаг сетки.

В соответствии с методом Рунге – Кутта четвертого порядка будем строить приближенное решение j_h(x) задачи (5.3.1) - (5.3.2) по правилу:

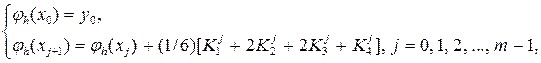
(5.4.4)

где

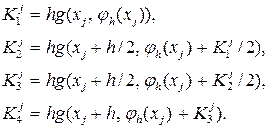(5.4.5)

В отличие от рассмотренных ранее разностных методов Эйлера и Адамса, в методе (5.4.4), (5.4.5) вычисления осуществляются не только в узлах сетки h_x, но и в промежуточных точках.

Результаты вычислений методом Рунге – Кутта удобно записывать
в таблицу, аналогичную табл. 5.4.1.

Таблица 5.4.1

j	x	y	K = hg(x, y)	aK
	x0	jh(x0)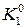
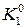
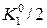
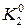
x0 + (h/2)	jh(x0) +		2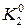
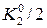
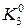
x0 + (h/2)	jh(x0)+		2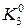
x0 + h	jh(x0) +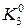
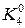
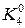
jh(x1) = jh(x0) + Djh(x0)	Djh(x0)
	x1	jh(x1)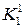
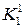
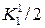
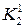
x1 + (h/2)	jh(x1) +		2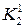
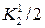
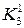
x1 + (h/2)	jh(x1) +		2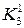
x1 + h	jh(x1) +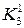
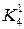
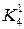
jh(x2) = jh(x1) + Djh(x1)	Djh(x1)
…	…	…	…	…

В заключение сделаем несколько замечаний относительно метода Рунге - Кутта.

1. Относится к семейству методов Рунге - Кутта четвертого порядка. (Более подробно с методами Рунге - Кутта можно ознакомиться в литературе по вычислительной математике.)

2. Метод сходится на отрезке [a, b] в соответствии с определением и имеет четвертый порядок точности.

3. Относительно большое количество вычислений, необходимых для определения приближенных значений искомой функции в каждом узле сетки h_x, при использовании метода (5.1.4), (5.1.5) компенсируется возможностью достижения необходимой точности в точке b при достаточно большом шаге h, что уменьшает количество узлов сетки.

4. Метод может быть легко адаптирован к решению задачи Коши для систем обыкновенных дифференциальных уравнений первого порядка.

Рассмотрим систему из двух уравнений

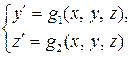
с начальными условиями

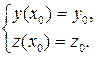
Будем искать решение поставленной задачи Коши на отрезке [a, b], задав на нем равномерную сетку h_x с шагом h.

Пусть функции j_{h, y}(x) » y(x) и j_{h, z}(x) » z(x) представляют собой приближенное решение задачи. Тогда метод Рунге - Кутта перепишется в виде

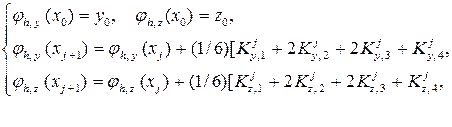
где

K_y,1^j = h g₁(x_j,j_h,y(x_j), j_h,z(x_j)),

K_z,1^j = h g₂(x_j,j_h,y(x_j), j_h,z(x_j)),

K_y,2^j = h g₁(x_j + h/2, j_{h, y}(x_j) + K_y,1^j/2, j_h,z(x_j) + K_z,1^j/2),

K_z,2^j = h g₂(x_j + h/2, j_{h, y}(x_j) + K_y,1^j/2, j_h,z(x_j) + K_z,1^j/2),

K_y,3^j = h g₁(x_j + h/2, j_h,y(x_j)+K_y,2^j/2,j_h,z(x_j)+K_z,2^j/2) ,

K_z,3^j = h g₂(x_j + h/2, j_h,y(x_j)+K_y,2^j/2,j_hz(x_j)+K_z,2^j/2) ,

K_y,4^j = h g₁(x_j + h, j_h,y(x_j) + K_y,3^j,j_h,z(x_j)+K_z,3^j) ,

K_z,4^j = h g₂(x_j+h,j_h,y(x_j)+K_y,3^j,j_h,z(x_j)+K_z,3^j) ,

j = 0, 1, 2, …, m - 1.

ЛИТЕРАТУРА

1. Бахвалов, Н.С. Численные методы в задачах и упражнениях : учеб. пособие / Н.С. Бахвалов, А.В. Лапин, Е.В. Чижонков : под ред. В.А. Садовничего. – М. : Высш. шк., 2000. – 190 с.

2. Бахвалов, Н.С. Численные методы : учеб. пособие для вузов / Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. - 8-е изд. - М., СПб. : Физматлит, 2000. - 624 с. : ил.

3. Боглаев, Ю.П. Вычислительная математика и программирование
/ Ю.П. Боглаев. – М. : Высш. шк., 1990. – 544 с.

4. Воробьева, Г.Н. Практикум по численной математике : учеб. пособие для сред. спец. учеб. завед. / Г.Н. Воробьева, А.Н. Данилова. – 2-е изд, перераб. и доп. - М. : Высш. шк., 1990. – 208 с.

5. Каханер, Д. Численные методы и программное обеспечение : пер.
с англ. / Д. Каханер, К. Моулер, С. Нэш. – 2-е изд., стеореотип. – М. : Мир, 2001. – 575 с. : ил.

6. Копченова, Н.В. Вычислительная математика в примерах и задачах / Н.В. Копченова, И.А. Марон. – М. : Наука, 1972 [и послед. издания]. - 368 с.

7. Самарский, А.А. Численные методы : учеб. пособие для вузов
/ А.А. Самарский, А.В. Гулин. – М. : Наука, 1989. – 432 с.

8. Середа, А.-В.И. Методы оптимизации : учеб.-метод. пособие : в 2 ч. Ч. 2. Нелинейное программирование. – Мурманск : Изд-во МГТУ, 1992. – 90 с.

[1] Здесь под экстремумом понимается только минимум функции.

[2] Если множество X замкнуто, то дополнительно вычисляются и значения функции f(x)
в граничных точках множества.

[3] Как и в гл. 1, под экстремумом здесь понимается только минимум функции.