Численное дифференцирование
Пусть на отрезке [a, b] в узлах одномерной сетки
hx ={xi / xi = xi–1 + hi, hi > 0, i = 1, 2, 3, …, n; x0 = a, xn = b}
заданы yi = f(xi), i = 0, 1, 2, …, n – значения дифференцируемой на этом отрезке функции f(x).
Для упрощения последующих записей будем считать, что сетка hx равномерная.
Поставим задачу вычисления приближенных значений производной функции f(x) в узлах сетки hx. Для ее решения можно воспользоваться определением производной, в соответствии с которым производная дифференцируемой в точке x функции f(x) может быть определена по правилу
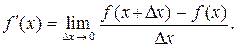 (4.2.1)
(4.2.1)
Производные в точках a и b (граничных точках отрезка) могут быть в этом случае определены как односторонние пределы:
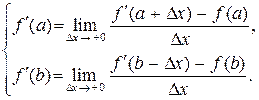 (4.2.2)
(4.2.2)
Здесь Dx ® +0 означает, что Dx стремится к нулю, оставаясь при этом больше нуля.
На основании (4.2.1) и (4.2.2) приближенные значения производных
в узлах сетки hx могут быть вычислены с помощью левостороннего, правостороннего и центрального конечно-разностных отношений соответственно:
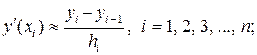 (4.2.3)
(4.2.3)
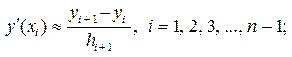 (4.2.4)
(4.2.4)
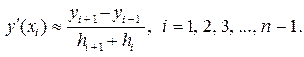 (4.2.5)
(4.2.5)
По формулам (4.2.3) и (4.2.4) определяют так называемые левостороннюю и правостороннюю разностные производные, по формуле (4.2.5) – центральную разностную производную.
Аналогично могут быть вычислены приближенные значения производных второго и более высоких порядков. Так, для определения производной второго порядка для i = 1, 2, …, n – 1 может быть использована следующая приближенная формула:
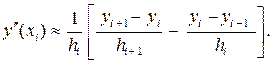 (4.2.6)
(4.2.6)
Пусть теперь d – абсолютная погрешность приведенных выше простейших формул численного дифференцирования. Здесь имеется в виду погрешность, возникающая при аппроксимации производной соответствующим конечно-разностным отношением, другими словами, погрешность метода. Для простоты при оценке погрешности аппроксимации сетку hx будем считать равномерной, с шагом h. Тогда для (4.2.3) и (4.2.4) имеет место оценка
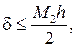 (4.2.7)
(4.2.7)
где M2 – максимум модуля производной второго порядка функции f(x) на отрезке [a, b].
Согласно (4.2.7) формулы (4.2.3) и (4.2.4) имеют погрешность первого порядка малости по h и точны (d = 0) для полиномов до первого порядка включительно.
Для формулы (4.2.5) оценка погрешности
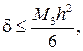 (4.2.8)
(4.2.8)
где M3 – максимум модуля производной третьего порядка функции f(x) на отрезке [a, b].
Согласно (4.2.8) формула (4.2.5) имеет погрешность второго порядка малости по h и точна (d = 0) для полиномов до второго порядка включительно.
Из приведенных выше теоретических оценок погрешности метода для формул (4.2.3)–(4.2.5) следует, что при стремлении шага сетки h к нулю погрешность получаемого приближенного значения производной также будет стремиться к нулю. Однако на практике этого не происходит, напротив, при h ® 0 погрешность получаемых результатов численного дифференцирования может неограниченно возрастать. Это происходит потому, что в соотношениях (4.2.7) и (4.2.8) оценивается только та часть погреш-ности, которая имеет место из-за замены производной конечно-разностным отношением и называется погрешностью аппроксимации. Другая часть результирующей погрешности обусловлена погрешностью производимых вычислительных операций над имеющими ненулевую погрешность данными значениями функции f(x) в узлах сетки hx.
Действительно, пусть абсолютная погрешность yi, i = 0, 1, 2, …, n может быть оценена сверху числом s > 0. Тогда в результате вычисления конечно-разностного отношения, например, по формуле (4.2.3) будет
получен результат, имеющий абсолютную вычислительную погрешность, которая может быть оценена сверху числом 2s / h. Значение s не зависит от h, и при h ® 0 оценка 2s / h неограниченно возрастает. Аналогично может быть проанализировано поведение вычислительной погрешности при определении конечно-разностных отношений по формулам (4.2.4) и (4.2.5).
Другими словами, при наличии ненулевой погрешности данных yi,
i = 0, 1, 2, …, n, представляющих собой значения функции f(x) в узлах сетки hx, суммарная погрешность приближенного расчета производных (складывается из погрешности аппроксимации и вычислительной погрешности) с помощью конечно-разностных отношений (4.2.3) – (4.2.5) может неограниченно возрастать при стремлении шага сетки к нулю. В связи с отмеченными свойствами погрешности операция численного дифференцирования в вычислительном отношении является некорректной.
С практической точки зрения при вычислениях по формулам
(4.2.3) – (4.2.5) необходимо стремиться к тому, чтобы вычислительная погрешность не превосходила погрешности аппроксимации. Применительно к формуле (4.2.3) это означает, что должно выполняться неравенство
(2s / h) £ (M2h / 2). (4.2.9)
Это неравенство может служить основанием для задания s – требуемой точности вычисления значений функции f(x) в узлах сетки hx, если шаг h сетки задан, или для определения минимально допустимого значения h, если значение s не может быть изменено. Например, из (4.2.9) следует, что s не должно превышать значения M2h2 / 4.
В целом организация вычислений приближенного значения производной с использованием одной из формул (4.2.3) – (4.2.5) очевидна и не вызывает затруднений. Вместе с тем необходимо отметить, что эти простейшие формулы численного дифференцирования позволяют вычислять приближенное значение производной f(x) только в узлах сетки hx и не позволяют производить вычисления в произвольной точке x* Î (a, b), не совпадающей ни с одним из этих узлов. Единственное, что можно предпринять для произвольной точки x* Î (a, b), это проинтерполировать по двум (или более) соседним с x* узлам сетки hx те приближенные значения производных, которые будут найдены в этих узлах по одной из формул (4.2.3) – (4.2.5). При этом нет смысла добиваться большей точности интерполирования, чем точность приближенного дифференцирования.
Имеется более общий подход к приближенному вычислению производных для таблично заданных функций, который заключается в использовании интерполяционного полинома. Действительно, если для заданной
в узлах сетки hx функции f(x) известен интерполяционный полином
Pn(x) = a0 + a1x + a2x2 + … + anxn, (4.2.10)
то, полагая, что функция f(x) m раз (m £ n) дифференцируема на отрезке [a, b], производную f(m)(x*) в любой точке x* Î [a, b] можно приближенно вычислить как производную соответствующего порядка интерполяционного полинома Pn(x):
f(m)(x*) » Pn(m)(x*). (4.2.11)
Погрешность нахождения производной по формуле (4.2.11) определяется модулем производной соответствующего порядка от Rn(x*) – остаточного члена интерполяции, задаваемого в соответствии с соотношением
f(x) = Pn(x) + Rn(x), x Î [a, b]. (4.2.12)
Важно отметить, что в общем случае из малости значений Rn(x)
не следует малость значений производных от Rn(x) и погрешность численного дифференцирования, как правило, превышает погрешность интерполяции.
Пусть на произвольном отрезке [xi – 1, xi + 1] Ì [a, b] по точкам xi – 1, xi
и xi + 1 построен интерполяционный полином в форме Лагранжа (формула (3.2.9)):
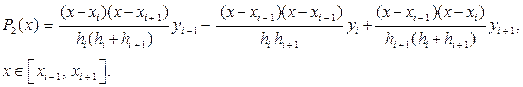 (4.2.13)
(4.2.13)
Для отыскания приближенного значения производной в произвольной точке x Î [xi – 1, xi + 1] в соответствии с (4.2.11) найдем выражение для первой производной P2(x):
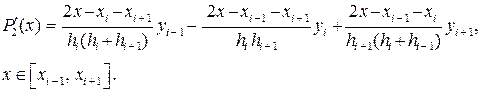 (4.2.14)
(4.2.14)
Если x = xi, получим
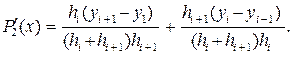 (4.2.15)
(4.2.15)
В случае равномерной сетки формула (4.2.15) и формула центральной разностной производной (4.2.5) эквивалентны.
Теперь для приближенного вычисления производных воспользуемся интерполяционным полиномом в форме Ньютона (формула (3.3.1)). Обозначим через Dmyi табличные (конечные) разности m-го порядка в i-m узле сетки hx:
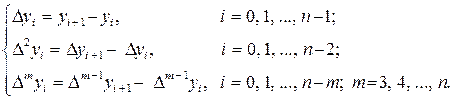 (4.2.16)
(4.2.16) 

Для упрощения записи у конечной разности первого порядка верхний индекс опускается.
Предположим, что сетка hx равномерная, и введем обозначение
z: = (x – x0) / h, x Î [a, b]. (4.2.17)
Тогда интерполяционный полином в форме Ньютона можно представить как
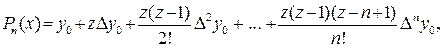 (4.2.18)
(4.2.18)
а приближенное равенство (4.2.11) для первой производной перепишется (для полинома, построенного по пяти узлам) в виде
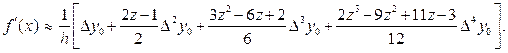 (4.2.19)
(4.2.19)
Если x совпадает с одним из узлов сетки hx, то этот узел всегда можно принять за x0. Тогда x = x0, z = 0 и формула (4.2.19) существенно упростится. Перепишем (4.2.19) для x = x0 в общем случае при интерполировании по (n + 1) узлу сетки:
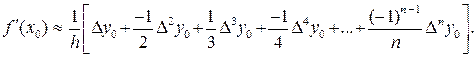 (4.2.20)
(4.2.20)
Очевидно, что при интерполировании по двум узлам (n = 1) фор-мула (4.2.20) эквивалентна формуле правосторонней разностной производной (4.2.4).
Погрешность аппроксимации производной функции f(m)(x) производной интерполяционного полинома Pn(m)(x) зависит от m-порядка производной и n-порядка полинома.
| Пусть погрешность аппроксимации d имеет k-й порядок по шагу h сетки, если d £ qhk, где q > 0 – ограниченная на промежутке интерполяции величина. |
Можно показать, что при аппроксимации первой производной функции f(x) первой производной интерполяционного полинома, построенного по двум узлам, погрешность аппроксимации будет первого порядка по h. Если использовать интерполяционный полином, построенный по трем узлам, то погрешность аппроксимации будет второго порядка по h.
Помимо погрешности аппроксимации заметное влияние на погрешность получаемых приближенных значений производной оказывает вычислительная погрешность. В частности, известно, что погрешность вычисления конечных разностей быстро увеличивается с ростом их порядка. Поэтому при расчетах с применением формул (4.2.19) и (4.2.20) в общем случае не следует использовать большое количество слагаемых, целесообразно ограничиваться лишь двумя, например:
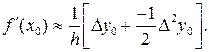 (4.2.21)
(4.2.21)
Для второй производной также можно использовать приближенное равенство
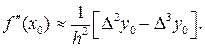 (4.2.22)
(4.2.22)
Пусть теперь заданы точка x* Î (a, b) и значения функции f(x) на отрезке [a, b] в узлах одномерной сетки hx. Для упрощения записи будем считать, что x* не совпадает ни с одним из узлов сетки. На основании проведенного анализа процесс приближенного вычисления производной функции f(x) в точке x* Î (a,b) с использованием интерполяционного полинома в форме Ньютона (оставляя два слагаемых в формуле (4.2.19)) можно представить, например, в виде следующего алгоритма:
1. На отрезке [a, b] задать одномерную равномерную сетку
hx = {xi / xi = xi – 1 + h, h > 0, i = 1, 2, 3, …, n; x0 = a, xn = b}
и значения yi = f(xi) в узлах сетки xi, i = 0, 1, 2, …, n.
Задать x* Î (a, b), x* ¹ xi, i = 0, 1, 2, …, n.
2. Определить узел xk сетки hx исходя из условий x* Î (xk, xk + 1);
0 £ k < n – 1.
3. Если xk найден, следует узлы xk, xk + 1, xk + 2 сетки hx обозначить как x0, x1, x2 соответственно и перейти к выполнению п. 5. Иначе – к выполнению п. 4.
4. Положить h: = –h. Узлы xn, xn – 1, xn – 2 сетки hx обозначить как x0, x1, x2 соответственно.
5. Вычислить z: = (x* – x0) / h.
6. Вычислить конечные разности Dy0 и D2y0.
7. Вычислить приближенное значение f¢(x) по формуле
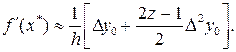
8. Процесс завершен.
Действия, выполненные в соответствии с п. 1 приведенного алгоритма, позволяют определить узел сетки, ближайший к целевой точке x* и находящийся на оси Ох левее этой точки. Выполнение условия 0 £ k < n – 1 обеспечивает возможность вычисления конечной разности второго порядка D2y0. Если такой узел xk не буден найден, это будет означать, что точка x* находится в нижней части таблицы и для решения задачи необходимо воспользоваться интерполяционным полиномом в форме Ньютона для интерполирования назад (п. 3).
В заключение дадим ряд практических рекомендаций по выполнению численного дифференцирования.
1. Вычисление конечных разностей удобно осуществлять в таблице, аналогичной табл. 4.2.1 для сетки с пятью узлами.
Таблица 4.2.1
| Номер узла | xi | F(xi) | Dyi | D2yi | D3yi | D4yi |
| x0 | f(x0) | |||||
| Dy0 | ||||||
| x1 | f(x1) | D2y0 | ||||
| Dy1 | D3y0 | |||||
| x2 | f(x2) | D2y1 | D4y0 | |||
| Dy2 | D3y1 | |||||
| x3 | f(x3) | D2y2 | ||||
| Dy3 | ||||||
| x4 | f(x4) |
2. Процедура численного дифференцирования является с вычислительной точки зрения некорректной. Для обеспечения вычислительной
устойчивости необходимо ограничивать снизу величину шага h сетки hx, не допуская ее неоправданного уменьшения.
3. На практике производные третьего и более высоких порядков численно определяются крайне редко из-за большой вычислительной погрешности получаемых результатов.
4. Использование интерполяционного полинома для реализации процедуры численного дифференцирования позволяет в общем случае достигать меньшей погрешности аппроксимации, чем применение простейших разностных отношений вида (4.2.3) – (4.2.5). Однако порядок интерполяционного полинома желательно ограничивать, не допуская применения полиномов более 5-го или 6-го порядков.
Дата добавления: 2021-07-22; просмотров: 912;











