Сплайн-интерполяция таблично заданной функции
Интерполяция таблично заданных функций с помощью сплайнов "лишена" главного недостатка полиномиальной интерполяции – роста степени интерполяционного полинома при увеличении количества узлов сетки. Сплайн-интерполяция представляет собой кусочно-полиномиальную интерполяцию, которая во многих случаях оказывается более эффективной, чем попытки подобрать один интерполяционный полином для отрезка [a, b], на котором представлены табличные данные. Следует отметить, что идеи использования кусочно-полиномиального приближения функций в вычислительной математике возникли достаточно давно. Классическим примером можно считать идеи, положенные в основу метода Эйлера для решения задачи Коши для обыкновенных дифференциальных уравнений первого порядка. Современная теория сплайн-интерполяции и прикладной математический аппарат для использования сплайнов с целью интерполяции и аппроксимации функций начали интенсивно развиваться с середины ХХ веке. В настоящее время это общепризнанное и все еще развивающееся направление вычислительной математики с достаточно широкой областью практического применения. При решении задач интерполяции преимущество сплайнов перед интерполяционными полиномами заключается в гарантированных устойчивости вычислительного процесса и сходимости сплайн-интерполяции при увеличении количества узлов сетки. В настоящем пособии рассмотрена задача интерполирования таблично заданной на отрезке [a, b] функции f(x) с использованием кубических сплайнов, которые широко применяются для интерполяции функций.
Пусть на отрезке [a, b] задана одномерная сетка
hx = {xi / xi = xi – 1 + hi, hi > 0, i = 1, 2, 3, …, n; x0 = a, xn = b},
в узлах xi которой заданы значения yi = f(xi), i = 0, 1, 2, …, n – соответствующие значения функции f(x). Очевидно, что все узлы сетки различны и упорядочены по возрастанию.
| Кубическим сплайном будем называть функцию S(x), заданную на отрезке [a, b] и удовлетворяющую следующим условиям: 1. S(xi) = yi, i = 0, 1, 2, …, n. 2. S(x), S ¢(x) и S ¢¢(x) непрерывны на отрезке [a, b]. На любом отрезке [xi – 1, xi], i = 1, 2, …, n S(x) представляет собой полином 3-й степени: Si(x) = ai + bi(x – xi) + (ci / 2)(x – xi)2 + (di / 6)(x – xi)3, x Î [xi – 1, xi], i = 1, 2, …, n. (3.4.1) |
Для построения кубического сплайна на отрезке [a, b] необходимо найти коэффициенты ai, bi, ci, di, i = 1, 2, …, n – всего 4n неизвестные величины. Для их нахождения в соответствии с определением кубического сплайна имеются условия:
– совпадения значений S(x) и таблично заданной функции f(x) в узлах сетки hx:
S(xi) = yi , i = 0, 1, 2, …, n;
– непрерывности функции S(x), ее первой и второй производных.
Эти условия сводятся к необходимости обеспечения непрерывности S(x) и ее производных во всех внутренних узлах (точках) xi, i = 1, 2, …,
n – 1 сетки hx, поскольку в этих точках происходит смена аналитического задания кусочно-полиномиальной функции S(x), в остальных точках отрезка [a, b] указанные функции непрерывны по определению.
Таким образом, для нахождения 4n неизвестных коэффициентов ai, bi, ci, di, i = 1, 2, …, n имеется только (n + 1) + 3(n – 1) = 4n – 2 условий. Два недостающих условия получаются из так называемых граничных условий, которые назначаются исходя из физических или других соображений, связанных с особенностями интерпретации таблично заданной функции f(x). Выберем в качестве граничных условий равенство нулю второй производной функции S(x) в граничных точках отрезка [a, b]:
S¢¢(a) = S¢¢(b) = 0.
В результате получим систему линейных уравнений из 4n уравнений для определения 4n неизвестных коэффициентов ai, bi, ci, di, i = 1, 2, …, n. Предварительный анализ этих уравнений и ряд несложных преобразований приводят к достаточно простой последовательности операций для нахождения значений указанных коэффициентов.
Коэффициенты ai, i = 1, 2, …, n определяются из соотношений
ai = yj, i = 1, 2, …, n. (3.4.2)
Для нахождения коэффициентов ci, i = 1, 2, …, n необходимо решить трехдиагональную систему линейных уравнений
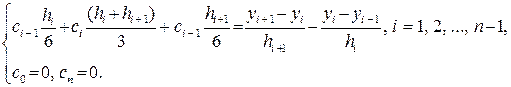 3.4.3)
3.4.3)
Очевидно, что эта система имеет матрицу с диагональным преобладанием, у нее единственное решение, для нахождения которого может быть использован метод прогонки.
После того как коэффициенты ci, i = 1, 2, …, n будут найдены, коэффициенты di, i = 1, 2, …, n могут быть определены по формуле
di = (ci – ci – 1) / hi, i = 1, 2, … (3.4.4)
Наконец, находим коэффициенты bi, i = 1, 2, …, n по формуле
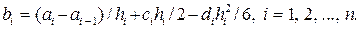 (3.4.5)
(3.4.5)
В результате вычислений будет построен интерполяционный кубический сплайн S(x).
Процесс интерполяции таблично заданной на отрезке [a, b] функции в заданную точку x* Î (a, b) с помощью интерполяционного кубического сплайна S(x) можно представить в виде следующего алгоритма:
0. На отрезке [a, b] задать одномерную сетку
hx = {xi / xi = xi –1 + hi, hi > 0, i = 1, 2, 3, …, n; x0 = a, xn = b}
и значения yi = f(xi) в узлах сетки xi, i = 0, 1, 2, …, n.
Задать x* Î (a, b).
1. Положить ai = yj, i = 0, 1, 2, …, n.
3. Составить и решить трехдиагональную систему (3.4.3) методом прогонки. Определить значения коэффициентов ci, i = 0, 1, 2, …, n.
4. Определить значения коэффициентов di и bi, i = 1, 2, 3, …, n, воспользовавшись формулами (3.4.4) и (3.4.5) соответственно.
5. Определить значение индекса 0 < k £ n из условия x* Î [xk – 1, xk].
6. Вычислить по формуле
S(x*) = Sk(x*) = ak + bk(x* – xk) + (ck / 2)(x* – xk)2 + (dk / 6)(x* – xk)3.
7. Процесс завершен: S(x*) – результат интерполяции табличных данных в точку x* Î (a, b).
Результаты расчета коэффициентов кубического сплайна удобно представлять в виде таблицы, аналогичной табл. 3.4.1.
Таблица 3.4.1
| k | xk | yk | ak | bk | Ck сk | dk |
| x0 | y0 | a0 | - | - | ||
| x1 | y1 | a1 | b1 | C1 | d1 | |
| x2 | y2 | a2 | b2 | C2 | d2 | |
| x3 | y3 | a3 | b3 | C3 | d3 | |
| … | … | … | … | … | … | … |
| n – 1 | xn – 1 | yn – 1 | an – 1 | bn – 1 | cn – 1 | dn – 1 |
| n | xn | yn | an | bn | dn |
Для визуальной оценки качества интерполирования желательно вычислить значения сплайна S(x) с достаточно малым шагом по переменной x и построить его график на отрезке [a, b], сопоставив с аналогичным графиком интерполяционного полинома Pn(x) и данными таблицы.
В заключение отметим некоторые характерные особенности использования кубических сплайнов для интерполяции табличных данных.
1. В случае равномерной сетки для погрешности интерполирования кубическими сплайнами может быть получена следующая оценка:
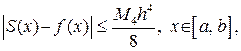 (3.4.6)
(3.4.6)
где M4 – максимум модуля четвертой производной интерполируемой функции на отрезке [a, b].
Предполагается, что на отрезке [a, b] функция f(x) непрерывна вместе со своими производными до 4-го порядка включительно. В соответствии с (3.4.6) погрешность интерполяции будет равна нулю, если интерполируемая функция представляет собой полином, степень которого
не превышает 3.
2. Интерполирование кубическими сплайнами является сходящейся процедурой в том смысле, что при стремлении максимального шага сетки к нулю (при этом, очевидно, неограниченно возрастает количество узлов сетки) погрешность сплайн-интерполяции равномерно стремится к нулю на отрезке [a, b] не только для интерполируемой функции f(x), но и для ее первых двух производных.
3. На практике часто не представляется возможным уменьшить шаг сетки, поскольку нет данных о значениях интерполируемой функции во вновь образующихся узлах. Поэтому сведения о сходимости и погрешности сплайн-интерполяции имеют прежде всего теоретическое значение. Однако всегда есть возможность оценить погрешность для фактически имеющейся сетки или сформулировать обоснованные требования к сбору данных (если такая возможность имеется) с учетом требуемой точности последующей интерполяции.
4. С увеличением количества узлов сетки hx на отрезке [a, b] степень используемых при сплайн-интерполяции полиномов не изменяется. Прямо пропорционально количеству узлов увеличивается только количество составляющих сплайн S(x) кубических полиномов Sk(x), k = 1, 2, 3, …, n. Как следствие, растет порядок решаемой для определения коэффициентов ci,
i = 0, 1, 2, …, n трехдиагональной системы линейных уравнений и общее количество вычислительных операций, требуемых для интерполирования табличных данных в заданную точку.
5. Как видно из описания построения кубического сплайна, он
не может быть однозначно определен из условий интерполяции; поэтому необходимо ввести два дополнительных условия, что создает определенные сложности при практической интерполяции. В любом случае при использовании стандартных компьютерных процедур сплайн-интерполяции желательно представлять, какие именно дополнительные условия в них используются. Кубический сплайн, при построении которого дополнительно вводятся условия
S ¢¢(a) = S ¢¢(b) = 0,
часто называют естественным.
6. Интерполирование с помощью сплайнов широко используется на практике. Однако нельзя сказать, что фактические результаты интерполяции всегда бесспорно удовлетворяют исследователей. Как отмечается
в литературе, имеется много случаев, когда сплайн не вполне удовлетворительно позволяет восстанавливать функции, для которых, например,
характерны быстрые изменения значений на малых промежутках. С целью устранения подобных недостатков разрабатываются различные модификации классических процедур, с которыми можно ознакомиться в соответствующей литературе.
§ 3.5. Аппроксимация таблично заданных функций
методом наименьших квадратов
Представим ситуацию, когда табличные данные имеют заметную вычислительную погрешность. В других случаях возникает необходимость подбора на основе имеющихся экспериментальных данных, представленных в табличной форме, некоторой функциональной зависимости из заданного класса функций, свойства которого наиболее соответствуют предполагаемым физическим свойствам изучаемых процессов или позволяют выявить характерную для этих процессов тенденцию. С математической точки зрения в этих и других возможных аналогичных случаях имеется функция с неизвестным (или известным, но слишком сложным с точки зрения проводимого исследования) аналитическим заданием, представленная в узлах заданной сетки значениями, которые были получены в результате прямых или косвенных измерений или некоторого вычислительного эксперимента. Такие данные будем называть экспериментальными. Поскольку по ряду причин (например, в силу большой погрешности) интерполирование такой таблично заданной функции не является целесообразным, ставится задача ее аппроксимации (замены) функцией из заданного класса, наиболее согласованной в смысле некоторого критерия с имеющимися экспериментальными данными. Подбираемую функцию будем называть моделью, а ее значения в узлах заданной сетки – модельными данными. Если в качестве критерия согласованности выбирается критерий минимума суммы квадратов отклонений модельных данных от экспериментальных, говорят об аппроксимации таблично заданной функции методом наименьших квадратов (МНК).
Формальная постановка задачи осуществляется следующим образом. Пусть на отрезке [a, b] задана одномерная сетка
hx = {xi / xi = xi – 1 + hi, hi > 0, i = 1, 2, 3, …, n; x0 = a, xn = b},
в узлах xi которой заданы значения yi = f(xi), i = 0, 1, 2, …, n – соответствующие значения функции f(x).
Пусть также для аппроксимации табличных данных выбран некоторый класс функций j (х, c0, c1, c2, …, cm), m < n, где c0, c1, c2, …, cm – неопределенные коэффициенты, выбор значений которых позволяет определить конкретную функцию из выбранного класса. Требуется найти значения коэффициентов c0, c1, c2,…, cm, для которых выполнено условие
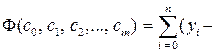 j (хi, c0, c1, c2, …, cm))2 Þ min. (3.5.1) j (хi, c0, c1, c2, …, cm))2 Þ min. (3.5.1)
|
Критерий (3.5.1), на основании которого осуществляется выбор значений коэффициентов c0, c1, c2, …, cm, является стандартным, используемым в МНК. Выбранные в соответствии с этим критерием значения коэффициентов позволяют определить среди множества функций конкретную функцию, наиболее согласованную с табличными (экспериментальными) данными или, иначе, обеспечивающую наилучшее среднеквадратическое приближение.
Как отмечалось выше, функция j (х, c0, c1, c2, …, cm) называется моделью, тогда коэффициенты c0, c1, c2,…, cm будем называть параметрами
модели или модельными. В дальнейшем ограничимся рассмотрением случая, когда модель линейно зависит от параметров и ее можно представить в виде
j (х, c0, c1, c2, …, cm) = c0j0(х) + c1j1(х) + c2j2(х) + … + cmjm(х). (3.5.2)
Модель вида (3.5.2) часто называют обобщенным полиномом. Здесь j0(х), j1(х), j2(х), jm(х) – множество так называемых базисных функций. Базисные функции могут быть как линейными, так и нелинейными функциями переменной x. Независимо от этого модель (3.5.2) остается линейной, поскольку она линейно зависит от модельных параметров c0, c1, c2, …, cm.
В качестве базисных могут быть выбраны, например, степенные функции
j0(х) = 1, j1(х) = х, j2(х) = х2, …, jm(х) = хm.
Тогда модель будет представлять собой полином степени m:
j (х, c0, c1, c2, …, cm) = c0 + c1х + c2х2 + … + cmхm. (3.5.3)
Очевидно, что в качестве базисных могут быть использованы и другие функции, необходимо лишь, чтобы они были линейно независимыми.
Итак, для линейной модели (3.5.2) требуется найти значения модельных параметров c0, c1, c2, …, cm, обеспечивающих выполнение условия (3.5.1). Эту задачу можно решить двумя способами.
Первый способ
С математической точки зрения поставленная задача является задачей безусловной минимизации функции нескольких переменных. Функция F(c0, c1, c2, …, cm) является квадратической одноэкстремальной, поэтому ее минимум можно искать, исходя из необходимых условий экстремума для функций нескольких переменных.
Запишем эти условия:
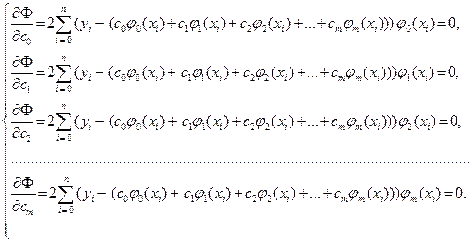 (3.5.4)
(3.5.4)
Сократив на 2, преобразуем систему линейных уравнений (3.5.4) к виду
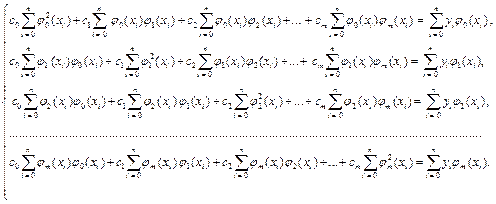 (3.5.5)
(3.5.5)
Уравнения (3.5.5) называют нормальными. Матрица системы линейных уравнений (3.5.5) имеет вид
Г = 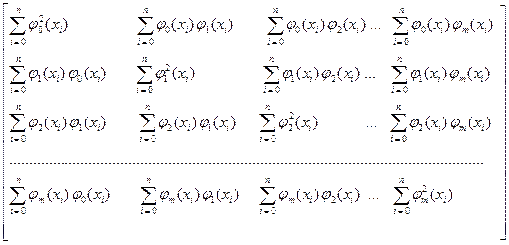 (3.5.6)
(3.5.6)
Матрицу Г называют матрицей Грамма.
Введем обозначения:
ji = (ji(х0), ji(х1), ji(х2), …, ji(хn))т, i = 0, 1, 2, …, m, (3.5.7)
y = (y0, y1, y2, …, yn)т; c = (c0, c1, c2, …, cm)т.
Тогда матрицу Грамма можно записать в более традиционном виде
Г = 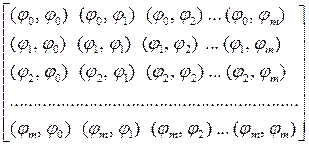 , (3.5.8)
, (3.5.8)
а систему (3.5.6) – в матричной форме
Гc = g. (3.5.9)
Здесь (ji, jk), i, k = 0, 1, 2, …, m – cкалярное произведение векторов ji и jk;
g = (g0, g1, g2, …, gm)т; gi = (y, ji), i = 0, 1, 2, …, m. (3.5.10)
Очевидно, что матрица Г симметричная. Можно показать, что она положительно определенная. Определитель матрицы Г (определитель Грамма) отличен от нуля в силу линейной независимости базисных функций j0(х), j1(х), j2(х), jm(х). Следовательно, система (3.5.4) имеет единственное решение, которое может быть найдено любым из известных методов решения систем с симметричной положительно определенной матрицей. В результате решения системы (3.5.4) будут найдены значения модельных параметров 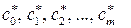 и определена наилучшая в смысле МНК модель j (х,
и определена наилучшая в смысле МНК модель j (х, 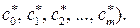
Процесс построения наилучшей в смысле метода наименьших квадратов аппроксимации таблично заданной на отрезке [a, b] функции можно представить в виде следующего алгоритма.
Метод 1
Первый способ
1. На отрезке [a, b] задать одномерную сетку
hx = {xi / xi = xi – 1 + hi, hi > 0, i = 1, 2, 3, …, n; x0 = a, xn = b}
и значения yi = f(xi) в узлах сетки xi, i = 0, 1, 2, …, n.
2. Задать систему базисных функций j0(х), j1(х), j2(х), jm(х).
3. В соответствии с (3.5.7) рассчитать компоненты векторов ji,
i = 0, 1, 2, …, m.
4. Руководствуясь (3.5.8) и (3.5.10), вычислить элементы матрицы Г
и компоненты вектора g.
5. Определить с = 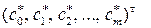 – вектор параметров модели (3.5.2) как решение системы линейных уравнений (3.5.9).
– вектор параметров модели (3.5.2) как решение системы линейных уравнений (3.5.9).
6. Модель j (х, 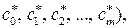 построенная согласно (3.5.2), является наилучшей в смысле МНК. Процесс завершен.
построенная согласно (3.5.2), является наилучшей в смысле МНК. Процесс завершен.
Оставаясь в рамках всех сделанных ранее предположений, рассмотрим теперь второй способ решения задачи (3.5.1).
Второй способ
Поскольку модель (3.5.2)
j (х, c0, c1, c2, …, cm) = c0j0(х) + c1j1(х) + c2j2(х) + … + cmjm(х)
должна соответствовать yi = f(xi), i = 0, 1, 2, …, n – данным, представленным в узлах сетки
hx = {xi / xi = xi – 1 + hi, hi > 0, i = 1, 2, 3, …, n; x0 = a, xn = b},
то значения модельных параметров вполне целесообразно выбирать из интерполяционных условий
j (хi, c0, c1, c2,…, cm) = yi, i = 0, 1, 2, …, n.
Эта система уравнений является системой линейных уравнений, поскольку модель j (хi, c0, c1, c2, …, cm) линейна относительно модельных параметров c0, c1, c2,…, cm. Запишем ее в детальной форме:
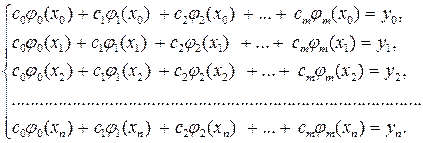 (3.5.11)
(3.5.11)
Матрица системы (3.5.11) – прямоугольная n×m матрица:
А = 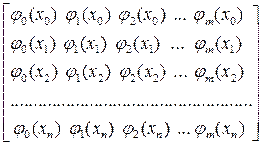 (3.5.12)
(3.5.12)
Система линейных уравнений (3.5.11) является переопределенной
с матрицей A, имеющей полный столбцовый ранг, так как по предположению m < n, а базисные функции j0(х), j1(х), j2(х), jm(х) линейно независимы. Как известно, для переопределенных систем линейных уравнений ищется так называемое обобщенное решение, которое обеспечивает минимум суммы квадратов невязок
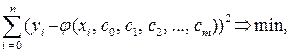
что соответствует условию (3.5.1).
Другими словами, значения модельных параметров 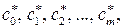 определяющие наилучшее среднеквадратическое приближение
определяющие наилучшее среднеквадратическое приближение
j (х, 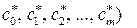 в соответствии с условием (3.5.1), могут быть определены как компоненты обобщенного решения переопределенной системы (3.5.11).
в соответствии с условием (3.5.1), могут быть определены как компоненты обобщенного решения переопределенной системы (3.5.11).
Для построения обобщенного решения системы (3.5.11) может быть использована первая трансформация Гаусса. В этом случае (3.5.11) преобразуется в систему (3.5.9). Действительно, применяя к системе (3.5.11) первую трансформацию Гаусса, получаем систему линейных уравнений
с квадратной неособенной матрицей
АтА c = Ат y.
Поскольку в обозначениях (3.5.7) и (3.5.8) Атy = g, а АтА = Г, полученная система эквивалентна системе (3.5.9).
Так как первая трансформация Гаусса ухудшает обусловленность системы линейных уравнений, то применение такого подхода не всегда целесообразно. В ряде случаев систему (3.5.11) предпочтительнее решать с помощью любого другого из известных методов, например с использованием ортогональных преобразований, что обеспечит большую устойчивость вычислительного процесса. В последнем случае процесс построения наилучшей в смысле метода наименьших квадратов аппроксимации таблично заданной на отрезке [a, b] функции можно представить в виде следующего алгоритма.
Метод 2
1. На отрезке [a, b] задать одномерную сетку
hx = {xi / xi = xi – 1 + hi, hi > 0, i = 1, 2, 3, …, n; x0 = a, xn = b}
и значения yi = f(xi) в узлах сетки xi, i = 0, 1, 2, …, n.
2. Задать систему базисных функций j0(х), j1(х), j2(х), jm(х).
3. Вычислить jk(хi), k = 0, 1, 2, …, m; i = 0, 1, 2, …, n – значения базисных функций в узлах сетки hx и в соответствии с (3.5.12) сформировать матрицу A.
4. Определить с = ( 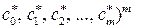 – вектор параметров модели (3.5.2) как обобщенное решение системы линейных уравнений (3.5.11). Решать систему (3.5.11) можно помощью одного из методов, использу-ющих ортогональные преобразования.
– вектор параметров модели (3.5.2) как обобщенное решение системы линейных уравнений (3.5.11). Решать систему (3.5.11) можно помощью одного из методов, использу-ющих ортогональные преобразования.
5. Модель j (х, 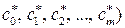 , построенная согласно (3.5.2), является наилучшей в смысле МНК. Процесс завершен.
, построенная согласно (3.5.2), является наилучшей в смысле МНК. Процесс завершен.
В заключение сделаем несколько замечаний по поводу рассмотренных методов.
1. В случае когда m – число модельных параметров будет равно n – количеству узлов сетки hx, наилучшая в среднеквадратическом смысле модель j (х, 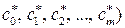 будет интерполяционной.
будет интерполяционной.
2. Метод 1 может быть предпочтительней метода 2при m << n.
В этом случае преимущество первого метода будет заключаться в небольшой размерности системы линейных уравнений (3.5.9) по сравнению с системой (3.5.11).
3. Метод 2, очевидно, будет предпочтительней метода 1 при
не очень хорошей или плохой обусловленности матрицы (3.5.12). В этом случае вычислительная устойчивость процесса будет в большей степени гарантирована при решении системы (3.5.11) без применения первой трансформации Гаусса.
В данной работе рассмотрена линейная задача, решенная методом наименьших квадратов. Довольно часто встречаются и нелинейные задачи МНК. Принципиально нелинейная задача решается аналогично линейной, но вместо линейных систем уравнений приходится решать нелинейные.
В целом следует отметить большую практическую значимость решения проблемы аппроксимации функций и МНК.
Глава 4. Численное дифференцирование
и интегрирование функций
Основные понятия
Численное дифференцирование является одной из важнейших вычислительных операций. Это объясняется тем, что достаточно много вычислительных алгоритмов предполагает вычисление и использование производных различного порядка от исследуемых функций. При этом довольно распространенной является ситуация, когда аналитическое задание функции, производные которой требуется найти, либо слишком сложное, либо вообще отсутствует, что не позволяет использовать аппарат аналитического дифференцирования и остается лишь возможность численного нахождения производных. Методы численного дифференцирования рассматриваются в § 4.2.
Другой важной в практическом отношении является задача вычисления определенных интегралов. При решении этой задачи, так же как и при численном дифференцировании, очень часто не представляется возможным найти определенный интеграл с помощью аналитических методов и приемов интегрального исчисления ввиду отсутствия аналитического задания функции либо его чрезмерная сложность для интегрирования. Кроме того, существуют так называемые неберущиеся итегралы. Это объясняется тем, что не для всех интегрируемых функций первообразная может быть представлена в конечном виде. Зачастую для нахождения определенных интегралов можно использовать только численное интегрирование. Формулы численного интегрирования называются квадратурными. (Методы численного интегрирования и некоторые аспекты их практического применения рассматриваются в § 4.3 и 4.4.)
Как и ранее, будем исходить из табличных значений исследуемой функции f(x) на некотором отрезке [a, b]. Другими словами, будем считать, что значения функции f(x) на отрезке [a, b] заданы в узлах одномерной сетки
hx ={xi / xi = xi–1 + hi, hi > 0, i = 1, 2, 3, …, n; x0 = a, xn = b}, (4.1.1)
где xi, i = 0, 1, 2, …, n – узлы одномерной сетки; hi, i = 1, 2, 3, …, n – ее шаг.
Если hi = h " i = 1, 2, 3, …, n, сетка hx равномерная.
Дата добавления: 2021-07-22; просмотров: 813;











