Дифференцирование комплексных функций
Функция 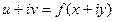 фактически задаёт отображение плоскости в плоскости, то есть пара действительных чисел
фактически задаёт отображение плоскости в плоскости, то есть пара действительных чисел 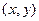 отображается в пару чисел
отображается в пару чисел 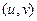 . Для двух функций
. Для двух функций 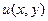 и
и 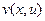 существуют 4 частных производных:
существуют 4 частных производных: 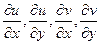 .
.
Определение производной. Производной функции 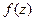 в точке
в точке 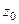 называется следующий предел:
называется следующий предел: 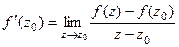 .
.
Также можно кратко записать в виде 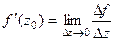 .
.
Заметим, что все величины в этой дроби, существуют и вычислимы, ведь здесь частное от разностей комплексных чисел.
Определение дифференцируемости.Функция 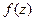 называется дифференцируемой в точке
называется дифференцируемой в точке 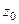 , если приращение функции можно представить в виде:
, если приращение функции можно представить в виде: 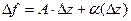 , где
, где 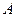 некоторое комплексное число,
некоторое комплексное число, 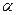 - бесконечно малая более высокого порядка, чем
- бесконечно малая более высокого порядка, чем  .
.
Заметим, что если функция дифференцируема, то 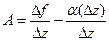 , но тогда т.е.
, но тогда т.е. 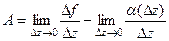 тогда
тогда 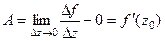 , т.е. константа
, т.е. константа 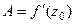 .
.
Геометрический смысл производной.Так как с точностью до бесконечно-малой, можно представить 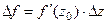 , а это линейное отображение, изученное в конце прошлой лекции, то в малой окрестности отображение представимо в виде растяжения и поворота, где
, а это линейное отображение, изученное в конце прошлой лекции, то в малой окрестности отображение представимо в виде растяжения и поворота, где 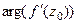 это угол поворота, а
это угол поворота, а 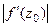 - коэффициент растяжения.
- коэффициент растяжения.
Изучим взаимосвязь дифференцируемости 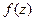 с дифференцируемостью координатных функций
с дифференцируемостью координатных функций 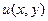 и
и 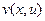 .
.
Теорема 1. Функция 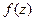 дифференцируема
дифференцируема 
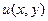 и
и 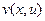 дифференцируемы и выполняются условия Коши-Римана:
дифференцируемы и выполняются условия Коши-Римана:
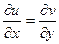 и
и 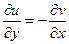 .
.
Доказательство.
Необходимость. Пусть функция дифференцируема, выведем условия Коши-Римана. Запишем подробнее равенство из определения дифференцируемости: 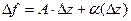 .
. 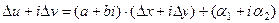 .
.
Раскроем скобки и сгруппируем слагаемые, в которых есть и в которых нет мнимой единицы.
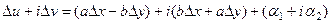
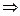
Получается такая система из двух равенств:
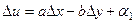
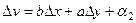
Выразим константу 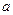 двумя способами из этих равенств. Если в 1-м уравнении задать приращение только по оси
двумя способами из этих равенств. Если в 1-м уравнении задать приращение только по оси 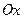 , тогда
, тогда 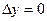 , то
, то 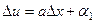
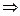
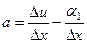
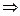
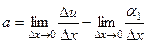 =
= 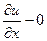 , так как
, так как 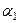 бесконечно малая более высокого порядка, так что при делении на величину
бесконечно малая более высокого порядка, так что при делении на величину 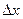 первого порядка предел равен 0.
первого порядка предел равен 0.
Итак, 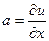 .
.
Если теперь во 2-м уравнении рассмотреть приращение только по оси 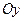 , то аналогично получится
, то аналогично получится 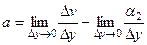 =
= 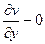 , т.е.
, т.е.  . Итак,
. Итак, 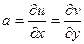 .
.
По аналогии с этими рассуждениями, если в 1-м равенстве вычислять предел при сдвиге только по оси 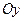 , а во 2-м по
, а во 2-м по 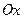 , получим
, получим
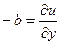 ,
, 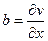 , откуда второе условие Коши-Римана
, откуда второе условие Коши-Римана 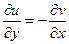 .
.
Достаточность.
Пусть выполнены условия Коши-Римана 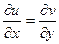 и
и 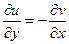 .
.
Тогда производная матрица отображения 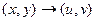 содержит не 4 разных константы, а две из них выражаются через две другие, то есть матрица имеет вид:
содержит не 4 разных константы, а две из них выражаются через две другие, то есть матрица имеет вид: 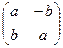 .
.
Тогда, с точностью до бесконечно-малых, 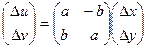 .
.
Тогда
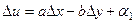
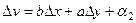 ,
,
Сложим эти 2 равенства, умножив при этом второе на 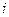 . Получим:
. Получим:
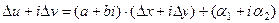 , то есть
, то есть 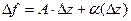 , что и означает дифференцируемость
, что и означает дифференцируемость 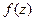 .
.
Теорема доказана.
Вывод. Итак, 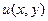 и
и 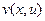 должны быть взаимосвязаны, т.е. если мы произвольно зададим две какие-то функции
должны быть взаимосвязаны, т.е. если мы произвольно зададим две какие-то функции 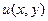 ,
, 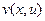 и составим из них
и составим из них 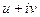 , то не всегда получим какую-то дифференцируемую комплексную функцию.
, то не всегда получим какую-то дифференцируемую комплексную функцию.
Пример.Проверить выполнение условий Коши-Римана для функции 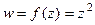 .
.
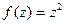 =
= 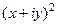 =
= 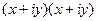 =
= 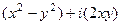 .
.
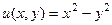 ,
, 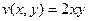 .
.
 ,
, 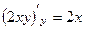 они равны (1-е условие Коши-Римана).
они равны (1-е условие Коши-Римана).
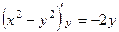 ,
, 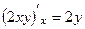 они противоположны ( а это и есть
они противоположны ( а это и есть
2-е условие Коши-Римана).
А сейчас мы рассмотрим функцию, для которой не выполнены условия Коши-Римана.
Пример. 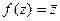 . Тогда
. Тогда 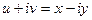 ,
, 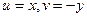 . Не выполняется 1-е условие:
. Не выполняется 1-е условие: 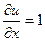 ,
, 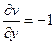 , они не равны ни в одной точке. Геометрически это означает, что зеркальное отражение плоскости невозможно представить в виде композиции растяжения и поворота, то есть невозможно равенство из условия дифференцируемости
, они не равны ни в одной точке. Геометрически это означает, что зеркальное отражение плоскости невозможно представить в виде композиции растяжения и поворота, то есть невозможно равенство из условия дифференцируемости 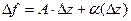 .
.
Дата добавления: 2020-03-17; просмотров: 892;











