Дифференцирование матриц

Пусть A(t) – матрица (m x n), элементы которой a_ij есть дифференцируемые функции скалярной переменной t. Производная от матрицы A(t) по переменной t есть матрица, элементами которой являются :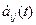

.

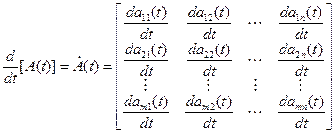Производная от суммыдвух матриц равна сумме производных от этих матриц:

.

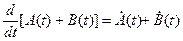Производная от произведенияматриц:

.

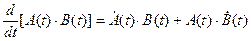При этом должен сохраняться первоначальный порядок следования сомножителей произведения.

.

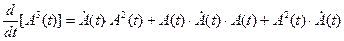Интегрирование матриц

Интеграл от матрицы определяется как матрица, образованная из интегралов от элементов исходной матрицы. Следовательно,

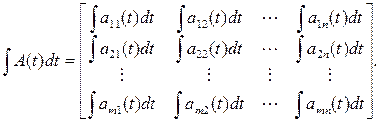
Для обозначения интеграла от матрицы обычно используется символ Q=∫ ( )dt. Если оператор Q снабжен индексами (сверху t, а снизу t₀), то они указывают нижний и верхний пределы интегрирования:

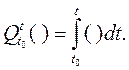
Пример 4. Найти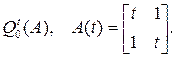

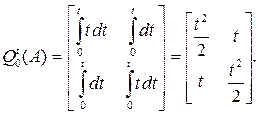
Определители

Определители существуют только для квадратных матриц.

В общем случае используется разложение Лапласа определителя n порядка по элементам строки (столбца) на сумму n определителей (n–1) порядка.

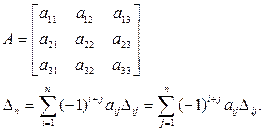
Например, для n = 3:

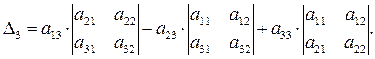
Свойства определителей