Вычитание множеств. Дополнение множества


Если заданы два множества, то можно не только найти их пересечение и объединение, но и вычесть из одного множества другое. Результат вычитания называют разностью и определяют следующим образом.

Определение. Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В.

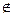Разность множеств А и В обозначают А \ В. Тогда, по определению, имеем: А\В={х |х А и х В}.

Если представить множества А и В при помощи кругов Эйлера, то разность А\В изобразится заштрихованной областью (рис. 10).

 

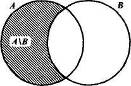
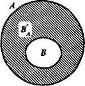
Рис. 10 Рис. 11

В школьном курсе математики чаще всего приходится выполнять вычитание множеств в случае, когда одно из них является подмножеством другого, при этом разность множеств А\В называют дополнением множества В до множества А, и обозначают символом В/А, а наглядно изображают так, как представлено на рисунке 11.

Определение. Пусть В с А. Дополнением множества В до множества А называется множество, содержащее те и только те элементы множества А, которые не принадлежат множеству В.

Как уже было сказано, в случае когда В 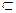A, A\B = В/А.

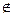Из определения следует, что В/А = {х | х А и х В}.

Выясним, как находить дополнение подмножества на конкретных примерах.

Если элементы множеств А и В перечислены и В 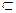А, то, чтобы найти дополнение множества В до множества А, достаточно перечислить элементы, принадлежащие множеству А и не принадлежащие множеству В. Так, если А = {1, 2, 3, 4, 5}, а В = {2,4},то В/А = {1,3,5}.

В том случае, когда указаны характеристические свойства элементов множеств А и В и известно, что В 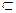А, то множество В/А задают также с помощью характеристического свойства, общий вид которого «х А и х 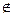В». Так, если А - множество четных чисел, а В - множество чисел, кратных 4, то В/А - это множество, содержащее такие четные числа, которые не делятся на 4. Например, 22 В/А, т.к. 22 А (т.е. оно четное) и 22 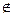В (т.е. оно не кратно 4).

Вычитание - это третья операция над множествами, с которыми мы уже познакомились. Нам известно, что пересечение множеств более сильная операция, чем объединение. А как быть с вычитанием? Например, каков порядок выполнения действий в выражении А\В С? Условились считать, что пересечение - более «сильная» операция, чем вычитание. Поэтому порядок выполнения действий в выражении А\В С такой: сначала находят пересечение множеств В и С, а затем полученное множество вычитают из множества А.

Что касается объединения и вычитания множеств, то их считают равноправными. Например, в выражении А\ В С надо сначала выполнить вычитание (из А вычесть В), а затем полученное множество объединить с множеством С.

Вычитание множеств обладает рядом свойств. В частности, можно доказать, что для любых множеств А, В и С справедливы следующие равенства:

1) (А\В)\С = (А\С)\В;

2) (А В) \С=(А\С) (В\С);

3) (А\В) С=(А С) \(В С);

4) А\(В С)=(А\В) (А\С);

5) А\(В С)+(А\В) (А\С).

 

Дата добавления: 2017-02-13; просмотров: 15014;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.011 сек.