Число элементов в декартовом произведении конечных множеств

Нам известно, как находят декартово произведение конечных множеств. Например, если А = {х, у, z }, В = { m, р }, то А х В= {(х, m), (х, р), (у, m), (у, р), (z, m), (z, р)}. Чтобы ответить на вопрос «Сколько элементов в полученном множестве?», - достаточно пересчитать их. А как определить число элементов в декартовом произведении множеств, не образуя его и не обращаясь к пересчету элементов?

Можно доказать, что если в множестве А содержится а элементов, а в множестве В - b элементов, то в декартовом произведении множеств А и В содержится a - b элементов, т.е.

n (АхВ)= n(А)· n (В)=а· b

Правило распространяется на случай t множеств, т.е. n (А₁х А₂ х ... хА _t,) = n (А₁,) · n (А₂) ·... · n (А_t,).

Например, если в множестве А содержится 3 элемента, в множестве В - 4 элемента, в множестве С- 5 элементов, то в их декартовом произведении будет содержаться 3·4·5 = 60 упорядоченных наборов из трех элементов.

Полученные формулы можно использовать при решении задач.

З а д а ч а 1. У Маши 3 различных юбки и 4 различных кофты. Сколько различных комплектов, состоящих из юбки и кофты, она может составить?

Р е ш е н и е. Пусть А - множество юбок у Маши, В - множество кофт у нее. Тогда, по условию задачи, n (А) = 3, n (В) = 4. Требуется найти число возможных пар, образованных из элементов множеств А и В, т.е. n (А х В). Но согласно правилу n (А х В) = n (А) · n (В) = 3·4 = 12. Таким образом, из 3 юбок и 4 кофт Маша может составить 12 различных комплектов.

З а д а ч а 2. Сколько двузначных чисел можно записать, используя цифры 5,4 и 7?

Р е ш е н и е. Запись любого двузначного числа состоит из двух цифр и представляет собой упорядоченную пару. В данном случае эти пары образуются из элементов множества А = {5, 4, 7}. В задаче требуется узнать число таких пар, т.е. число элементов в декартовом произведении А х А. Согласно правилу n (А х А) = n (А) · n (А) = 3·3 = 9. Значит, двузначных чисел, записанных с помощью цифр 5, 4 и 7, будет 9.

Часто при решении задач, аналогичных рассмотренным выше, требуется не только ответить на вопрос о том, сколько существует возможных вариантов ее решения, но и осуществить перебор этих вариантов. Например, в задаче 2 можно предложить записать все двузначные числа, используя цифры 5,4 и 7.

Существует единый подход к осуществлению такого перебора - строится схема, называемая деревом возможных вариантов. Так, для задачи 2 она будет иметь вид (рис. 25):

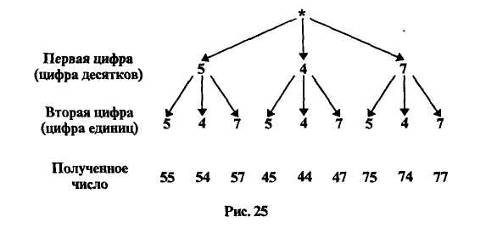
Эта схема действительно похожа на дерево, правда, растет оно вниз и у него нет ствола. То, что дерево растет как бы «вверх ногами», удобно при построении схем такого вида. Знак * изображает корень дерева, ветвями которого являются различные варианты решения задачи. Чтобы получить двузначное число, надо сначала выбрать цифру десятков - для этого есть три варианта: 5, 4 или 7. Поэтому из * проведены три отрезка и на их концах поставлены цифры 5, 4 и 7. Затем надо выбрать цифру единиц, а для этого также есть три варианта: 5, 4 или 7. Поэтому от цифр 5, 4 и 7 проведено по три отрезка, на концах которых опять стоят цифры 5, 4 или 7. Чтобы прочитать полученные варианты, надо пройти по всем ветвям построенного дерева сверху вниз.