Понятие разбиения множества на классы

Понятия множества и операций над множествами позволяют уточнить наше представление о классификации - действии распределения объектов по классам.

Классификацию мы выполняем достаточно часто. Так, натуральные числа представляем как два класса - четные и нечетные. Углы на плоскости разбиваем на три класса: прямые, острые и тупые.

Любая классификация связана с разбиением некоторого множества объектов на подмножества. При этом считают, что множество X разбито на классы X₁, Х₂,..., Х_п, если:

1) подмножества X₁, Х₂,..., Х_п попарно не пересекаются;

2) объединение подмножеств X₁, Х₂,..., Х_п совпадает с множеством X.

Если не выполнено хотя бы одно из условий, классификацию считают неправильной. Например, если из множества X треугольников выделить подмножества равнобедренных, равносторонних и разносторонних треугольников, то разбиения мы не получим, поскольку подмножества равнобедренных и равносторонних треугольников пересекаются (все равносторонние треугольники являются равнобедренными). В данном случае не выполнено первое условие разбиения множества на классы.

Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять мри помощи свойств элементов множеств.

Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Положим, что нас интересуют числа, обладающие свойством «быть кратным 3». Это свойство позволяет выделить из множества натуральных чисел подмножество, состоящее из чисел, кратных 3. Тогда

про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество множества натуральных чисел (рис. 12). Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством натуральных чисел, то имеем разбиение этого множества на два класса.

Вообще, если на множестве X задано одно свойство, то это множество разбивается на два класса. Первый- это класс объектов, обладающих этим свойством, а второй- дополнение первого класса до множества X. Во втором классе содержатся такие объекты множества X, которые заданным свойством не обладают. Такую классификацию называют дихотомической.

Рассмотрим теперь ситуацию, когда для элементов множества заданы два свойства. Например, какие свойства натуральных чисел, как «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества N натуральных чисел можно выделить дна подмножества: А - подмножество чисел, кратных 3, и В - подмножество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 13).

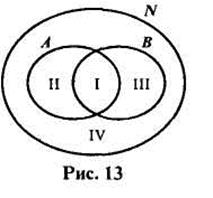
Проанализируем получившийся рисунок. Конечно, разбиения множества натуральных чисел на подмножества А и В не произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей - на рисунке они пронумерованы. Каждая область изображает некоторое подмножество множества N. Подмножество I состоит из чисел, кратных 3 и 5; подмножество II - из чисел, кратных 3 и не кратных 5; подмножество III -из чисел, кратных 5 и не кратных 3; подмножество IV- из чисел, не кратных 3 и не кратных 5. Объединение этих четырех подмножеств есть множество N.

Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.

Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. Например, при помощи таких двух свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается на три класса (рис. 14):

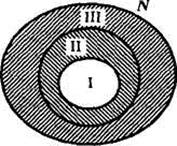
Рис. 14

I - класс чисел, кратных 6; II - класс чисел, кратных 3, но не кратных 6; III - класс чисел, не кратных 3.