Число элементов в объединении и разности конечных множеств

Нам известно, как находят объединение двух конечных непересекающихся множеств. Например, если А = {х, у, z}, а В = {к, l , m, р), то А В = {х, у, z, к, I, m , р}. Чтобы ответить на вопрос: «Сколько элементов в полученном множестве?» - достаточно пересчитать их.

А как определять число элементов в объединении конечных множеств, не образуя его и не обращаясь к пересчету элементов?

Условимся предложение «Множество А содержит а элементов» записывать в таком виде: n (А) = а. Например, если А = {х, у, z, } то утверждение «Множество А содержит три элемента» можно записать так: n (А) = 3.

Можно доказать, что если в множестве А содержится а элементов, а в множестве В – b элементов и множества А и В не пересекаются, то в объединении множеств А и В содержится а + Ъ элементов, т.е.

n (А В) = n (А) + n (В) = а + b (1).

Это правило нахождения числа элементов в объединении двух конечных непересекающихся множеств, его можно обобщить на случай t попарно непересекающихся множеств, т.е. если множества А₁, А₂, …, А _t, попарно не пересекаются, то n(A₁ А₂ ... А) = n (А₁) + n (А₂) + ... + n (А _t,).

Пусть, например, А = {х, у, г }, В = {к, I, т, р }, С = {q, s}. Найдем число элементов в объединении данных множеств.

Пересчитав элементы данных множеств, получаем, что n (А) =3, n (В) = 4, n(С) = 2. Видим, что А В = 0, А С = 0, В С = Ø, т.е. данные множества попарно не пересекаются. Тогда, согласно правилу нахождения числа элементов в объединении конечных множеств, получаем:

n (А В С) = n (А) + n (В) + n (С) = 3 + 4 + 2 = 9.

Таким образом, в объединении заданных трех множеств содержится 9 элементов.

Нетрудно убедиться в том, что если В 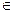А, то n (В^/_А) = n (А) – n (В), т.е. число элементов дополнения подмножества В до данного конечного множества А равно разности численностей этих множеств.

Пусть, например, А = {х, y, z, p, t}, а B = {х, p, t}.Найдем число элементов в дополнении подмножества В до множества А.

Пересчитав элементы множеств А и В, получаем, что n (А) = 5, n (В) = 3. Тогда n ( В^/_А) = n (А) - n (В) = 5-3 = 2. Таким образом, в дополнении множества В до множества А содержится два элемента.

Формула (1) позволяет находить число элементов в объединении конечных непересекающихся множеств. А если множества А и В имеют общие элементы, то как найти число элементов в их объединении?

Пусть, например, А = {х, у, z }, а В = {х, z, p, s, к}. Тогда А В = {х, у, z, р, s, к}, т.е. если n (А) = 3, а n (В) = 5 и А В ≠ Ø, то n (А В) = 6. Нетрудно видеть, что в данном случае n (А В) = 2 и, значит, общие элементы множеств А и В и объединении этих множеств записаны только один раз.

В общем виде правило подсчета элементов в объединении двух конечных множеств может быть представлено в виде формулы:

n (А В) = n (А) + n (В) - n (А В) (2).

Полученные формулы для подсчета числа элементов в объединении двух и более множеств можно использовать для решения текстовых задач следующего вида.

З а д а ч а 1. Из 40 студентов курса 32 изучают английский язык, 21 - немецкий язык, а 15- английский и немецкий языки. Сколько студентов курса не изучает ни английский, ни немецкий языки?

Р е ш е н и е. Пусть А- множество студентов курса, изучающих английский язык, В - множество студентов курса, изучающих немецкий язык. По условию задачи: n (А) = 32, n (В) = 21, n (А В) = 15. Требуется найти число студентов курса, не изучающих ни английского, ни немецкого языка.

1 способ.

1) Найдем число элементов в объединении данных множеств А и В. Для этого воспользуемся формулой (2):

n (А В) = n (А) + n (В) - n (А В) = 32 + 21 - 15 = 38.

2) Найдем число студентов курса, которые не изучают ни английский, ни немецкий языки: 40 - 38 = 2.

2 способ.

I) Изобразим данные множества при помощи кругов Эйлера и определим число элементов в каждом из непересекающихся подмножеств (рис. 23).

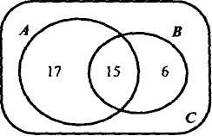Рис .23

n (С)=40

Так как в пересечении множеств А и В содержится 15 элементов, то студентов, изучающих только английский язык, будет 17 (32- 15 = 17), а студентов, изучающих только немецкий, - 6 (21 - 15 = 6). Тогда n (А 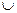В) = 17 + 15 + 6 = 38, и, следовательно, число студентов курса, которые не изучают ни английский, ни немецкий языки, будет 40 - 38 = 2.