Объединение множеств

Объединение множеств А и В обозначают А В. Таким образом, по определению, А В = {x|x А или х В}.

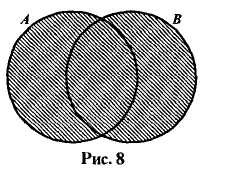
Если изобразить множества А и В при помощи кругов Эйлера, то объе­динение данных множеств изобразит­ся заштрихованной областью (рис. 8).

Выясним, как находить объедине­ние множеств в конкретных случаях.

Если элементы множеств А и В пе­речислены, то, чтобы найти А В,

достаточно перечислить элементы, которые принадлежат множеству А или множеству В.

А как быть, если множества заданы характеристическими свойствами их элементов? Из определения объединения следу­ет, что характеристическое свойство элементов множества А В составляется из характеристических свойств элементов множеств А и В с помощью союза «или». Найдем, например, объединение множества А - четных натуральных чисел и множества В - двузначных чисел. Так как свойство элементов множества А - «быть четным натуральным числом», а свойство элементов множества В - «быть двузначным числом», то в объ­единение данных множеств войдут числа, характеристическое свойство которых - «быть четным натуральным или двузнач­ным числом». Такие числа образуют бесконечное множество, но сформулированное характеристическое свойство позволяет однозначно определять, содержится тот или иной элемент в объединении множеств А и В или не содержится. Например, в A B есть число 8, поскольку оно четное; есть число 36 - оно четное и двузначное.

Рассмотрим теперь случай, когда находят объединение множества А и его подмножества В. Легко видеть, что тогда А В = А и, следовательно, характеристическое свойство элементов множества A В будет таким, как и свойство элементов множества А.