Алгебраические операции над нечеткими множествами

Алгебраическое произведение АиВобозначается A·В и определяется так: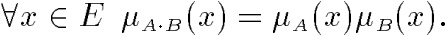

Алгебраическая сумма этих множеств обозначается А+ В и определяется так: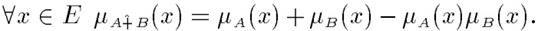

Для операций {-, +} выполняются свойства:

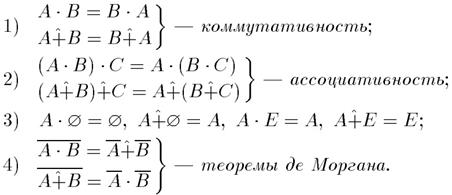
Не выполняются:

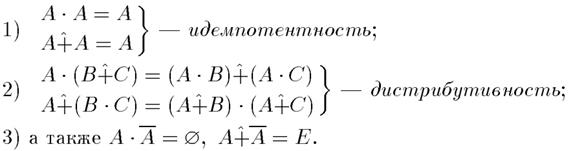
Замечание.При совместном использовании операций { U, ⋂, + , • } выполняются свойства:

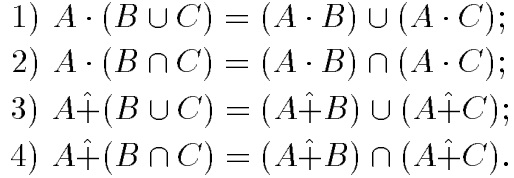
На основе операции алгебраического произведения определяется операция возведения в степень α нечеткого множества А,где α— положительное число. Нечеткое множество А^α определяется функцией принадлежности μ^α_A= μ^α_A(x). Частным случаем возведения в степень являются:

1) CON(А) = А² — операция концентрирования (уплотнения);

2) DIL(А) = А^0,5 — операция растяжения,

которые используются при работе с лингвистическими неопределенностями (рис. 1.4).

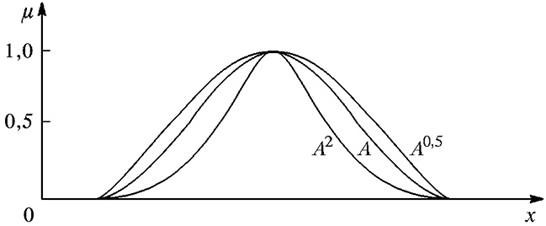
Рис. 1.4. Иллюстрация к понятию операций концентрирования (уплотнения) и растяжения

Умножение на число. Если α— положительное число, такое, что 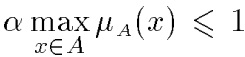, то нечеткое множество αА имеет функцию принадлежности:

μ_αА(х) = αμ_A(x).

Выпуклая комбинация нечетких множеств.Пусть A₁, А₂,..., А_n— нечеткие множества универсального множества Е, aω₁, ω₂, …, ω_n— неотрицательные числа, сумма которых равна 1.

Выпуклой комбинацией A₁, А₂, ..., А_nназывается нечеткое множество А с функцией принадлежности:

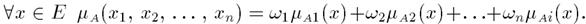
Декартово(прямое) произведение нечетких множеств.Пусть A₁, А₂, ..., А_n— нечеткие подмножества универсальных множеств Е₁, Е₂,…, Е_nсоответственно. Декартово, или прямое произведение А = А₁ x А₂ x... x А_n является нечетким подмно­жеством множества Е =Е₁ x Е₂ x... x Е_n с функцией принад­лежности:

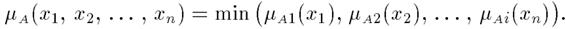
Оператор увеличения нечеткостииспользуется для преобразования четких множеств в нечеткие и для увеличения нечеткости нечеткого множества.

Пусть А — нечеткое множество, Е— универсальное множество и для всех хϵЕопределены нечеткие множества К(х).Совокуп­ность всех К(х)называется ядром оператора увеличения нечетко­сти Ф. Результатом действия оператора Ф на нечеткое множество Аявляется нечеткое множество вида

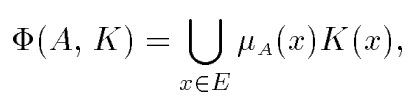
где μ_А(х)К(х)— произведение числа на нечеткое множество.

Пример.Пусть

Е ={1,2,3,4}; А = 0,8/1+ 0,6/2+ 0/3+ 0/4; К(1)=1/1 + 0,4/2;

К(2) = 1/2 + 0,4/1 + 0,4/3; К(3) = 1/3 + 0,5/4; К(4)= 1/4.

Тогда

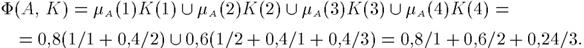
Четкое множество α-уровня(или уровня α). Множеством α-уровня нечеткого множества А универсального множества Е на­зываетсячеткое подмножество А_α универсального множества Е,определяемое в виде

А_α={ x/μ_A(x) ≥ α },

где α ≤ 1.

Пример.Пусть А = 0,2/x₁+ 0/x₂+ 0,5/x₃+ 1/x₄, тогда A_0,3={x₃,x₄},A_0,7 = {х₄ }.

Достаточно очевидное свойство: если α₁ ≥ 2, то А_α1≤ А_α2.