Глава 2. Операции над множествами
Множества можно определять также при помощи операций над некоторыми другими множествами. Пусть имеются два множества  и
и  .
.
Объединение (сумма) 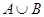 есть множество всех элементов, принадлежащих
есть множество всех элементов, принадлежащих  или
или  . Например,
. Например, 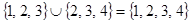 .
.
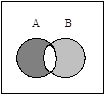
Пересечение (произведение) 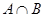 есть множество всех элементов, принадлежащих одновременно как
есть множество всех элементов, принадлежащих одновременно как  , так и
, так и  . Например,
. Например, 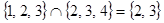 . Множества, не имеющие общих элементов
. Множества, не имеющие общих элементов 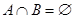 , называются непересекающимися.
, называются непересекающимися.
Разность 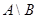 есть множество, состоящее из всех элементов
есть множество, состоящее из всех элементов  , не входящих в
, не входящих в  , например,
, например, 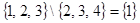 . Ее можно рассматривать как относительное дополнение
. Ее можно рассматривать как относительное дополнение  до
до  . Если
. Если 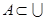 , то множество
, то множество 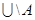 называется абсолютным дополнением множества
называется абсолютным дополнением множества  и обозначается через
и обозначается через 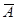 . Оно содержит все элементы универсума
. Оно содержит все элементы универсума 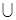 , кроме элементов множества
, кроме элементов множества  . Дополнение
. Дополнение  определяется отрицанием свойства
определяется отрицанием свойства 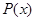 , с помощью которого определяется
, с помощью которого определяется  . Очевидно,
. Очевидно, 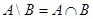 .
.
Дизъюнктивная сумма (симметрическая разность) 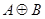 есть множество всех элементов, принадлежащих или
есть множество всех элементов, принадлежащих или  , или
, или  (но не обоим вместе). Например,
(но не обоим вместе). Например, 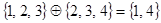 . Дизъюнктивная сумма получается объединением элементов множеств за исключением тех, которые встречаются дважды.
. Дизъюнктивная сумма получается объединением элементов множеств за исключением тех, которые встречаются дважды.
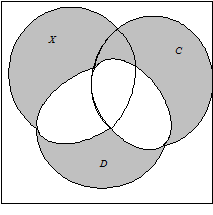
Для наглядного изображения соотношений между подмножествами какого-либо универсума 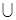 используют круги Эйлера (рис. 1).
используют круги Эйлера (рис. 1).
| 
| 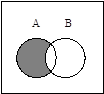
| 
|
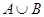
| 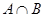
| 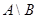
| 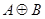
|
| Рис. 1 |
Обычно универсум представляется множеством точек прямоугольника, а его подмножества изображаются в виде кругов или других простых областей внутри этого прямоугольника.
Множества, получаемые в результате операций над множествами  и
и  , изображены на рис. 1 заштрихованными областями. Непересекающиеся множества изображаются неперекрывающимися областями, а включение множества соответствует области, целиком располагающейся внутри другой. Дополнение множества
, изображены на рис. 1 заштрихованными областями. Непересекающиеся множества изображаются неперекрывающимися областями, а включение множества соответствует области, целиком располагающейся внутри другой. Дополнение множества  (до
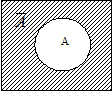
(до 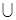 ), т. е. множество
), т. е. множество  изображается той частью прямоугольника, которая лежит за пределами круга, изображающего
изображается той частью прямоугольника, которая лежит за пределами круга, изображающего  (рис. 2).
(рис. 2).
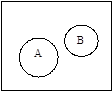
|
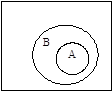
|
|
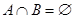
| 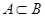
| 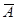
|
| Рис. 2 |
Операции над множествами, как и операции над числами, обладают некоторыми свойствами (табл. 1). Эти свойства выражаются совокупностью тождеств, справедливых независимо от конкретного содержания входящих в них множеств, являющихся подмножествами некоторого универсума 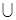 .
.
Тождества (1а) – (За) выражают соответственно коммутативный, ассоциативный и дистрибутивный законы для объединения, а тождества (1б) – (3б) – те же законы для пересечения. Соотношения (4а) – (7а) определяют свойства пустого множества 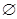 и универсума
и универсума 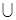 относительно объединения, а соотношения (4б) – (7б) – относительно пересечения.
относительно объединения, а соотношения (4б) – (7б) – относительно пересечения.
Выражения (8а) и (8б), называемые законами идемпотентности, позволяют записывать формулы с множествами без коэффициентов и показателей степени. Зависимости (9а) и (9б) представляют законы поглощения, а (10а) и (10б) – теоремы де Моргана.
Соотношения (11) – (20) отражают свойства дополнения, разности, дизъюнктивной суммы, включения и равенства.
| Таблица 1 | |||
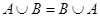
| (1а) | 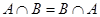
| (1б) |
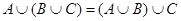
| (2а) | 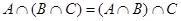
| (2б) |
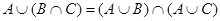
| (3а) | 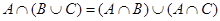
| (3б) |
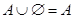
| (4а) | 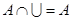
| (4б) |
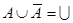
| (5а) | 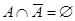
| (5б) |
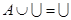
| (6а) | 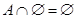
| (6б) |
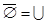
| (7а) | 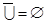
| (7б) |
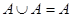
| (8а) | 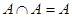
| (8б) |
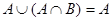
| (9а) | 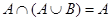
| (9б) |
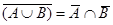
| (10а) | 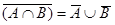
| (10б) |
если 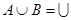 и и 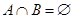 , то , то 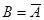
| |||
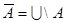
| |||
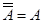
| |||
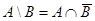
| |||
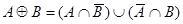
| |||
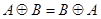
| |||
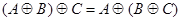
| |||
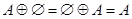
| |||
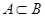 , если и только если , если и только если 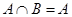 или или 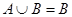 или или 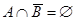
| |||
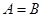 , если и только если , если и только если 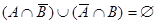
|
Первые десять свойств в табл. 1 представлены парами двойственных (дуальных) соотношений, одно из которых получается заменой в другом символов: 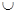 на
на 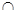 и
и 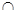 на
на 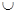 , а также
, а также 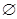 на
на 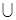 и
и 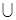 на
на 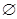 . Соответствующие пары символов
. Соответствующие пары символов 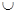 ,
, 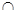 и
и 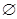 ,
, 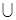 называются двойственными (дуальными) символами.
называются двойственными (дуальными) символами.
При замене в любой теореме входящих в нее символов дуальными получим новое предложение, которое также является теоремой (принцип двойственности или дуальности). Тождества (11) и (12) не изменяются при замене символов дуальными, поэтому их называют самодвойственными.
Принцип дуальности можно распространить на разность и дизъюнктивную сумму, если использовать тождества (14) и (15). Аналогично в соответствии с соотношением (19) можно заменить 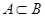 на
на 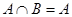 или
или 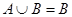 . Но поскольку дуальным
. Но поскольку дуальным 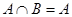 есть
есть 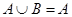 , то дуальным
, то дуальным 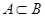 следует считать
следует считать 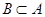 . Поэтому, расширяя принцип дуальности на выражения, в которые входит символ включения, необходимо при переходе к дуальному выражению все знаки
. Поэтому, расширяя принцип дуальности на выражения, в которые входит символ включения, необходимо при переходе к дуальному выражению все знаки 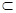 и заменить на
и заменить на 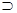 и обратно. Доказательство тождеств (табл. 1) основано на отношении принадлежности. Важно отметить, что любая теорема алгебры множеств и, в частности, соотношения, приведенные в табл. 1, выводимы из первых пяти свойств, которые в свою очередь доказываются только в терминах отношения принадлежности. Это можно рассматривать как иллюстрацию аксиоматического подхода к алгебре множеств.
и обратно. Доказательство тождеств (табл. 1) основано на отношении принадлежности. Важно отметить, что любая теорема алгебры множеств и, в частности, соотношения, приведенные в табл. 1, выводимы из первых пяти свойств, которые в свою очередь доказываются только в терминах отношения принадлежности. Это можно рассматривать как иллюстрацию аксиоматического подхода к алгебре множеств.
Алгебра множеств представляет собой теоретико-множественный аналог обычной алгебры действительных чисел и основана на свойствах операций над множествами. Одним из разделов алгебры множеств являются тождественные преобразования, с помощью которых можно упрощать или преобразовывать к удобному виду различные выражения, содержащие множества. Такие преобразования осуществляются последовательным применением соответствующих свойств операций над множествами.
Наряду с тождествами, справедливыми при любых значениях входящих в них множеств (подмножеств универсума 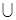 ), алгебра множеств рассматривает уравнения, которые содержат фиксированные подмножества
), алгебра множеств рассматривает уравнения, которые содержат фиксированные подмножества 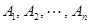 и подлежащие определению подмножества
и подлежащие определению подмножества 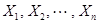 . В простейшем случае в уравнение входит одно такое подмножество
. В простейшем случае в уравнение входит одно такое подмножество 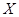 . Требуется ответить на вопрос, при каких условиях уравнение имеет решение и, если эти условия соблюдаются, найти все такие решения, т. е. определить
. Требуется ответить на вопрос, при каких условиях уравнение имеет решение и, если эти условия соблюдаются, найти все такие решения, т. е. определить 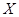 .
.
Решение уравнения с одним подмножеством 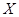 , подлежащим определению, основывается на последовательности тождественных преобразований:
, подлежащим определению, основывается на последовательности тождественных преобразований:
1. В соответствии со свойством 20 (табл. 1) равенство преобразуется в дизъюнктивную сумму его левой и правой частей, которая приравнивается пустому множеству.
2. Полученное уравнение преобразуется к виду 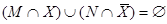 , где
, где 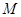 и
и 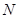 – некоторые множества, не содержащие
– некоторые множества, не содержащие 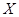 (можно показать, что любое уравнение с правой частью
(можно показать, что любое уравнение с правой частью 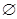 приводится к такому виду).
приводится к такому виду).
3. Так как объединение множеств пусто только при условии, что каждое из них также пустое множество, преобразованное уравнение запишем зависимой системой двух уравнений: 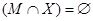 и
и 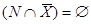 .
.
4. Пара уравнений (а следовательно, и исходное уравнение) имеет смысл тогда и только тогда, когда 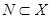 и
и 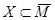 (свойство 19 табл. 1). Это значит, что условием существования решения является
(свойство 19 табл. 1). Это значит, что условием существования решения является 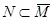 (свойство транзитивности отношения включения), а решением уравнения – любое множество
(свойство транзитивности отношения включения), а решением уравнения – любое множество 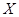 такое, что
такое, что 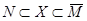 .
.
Графические методы алгебры множеств помимо кругов Эйлера используют также диаграммы Венна. Построение диаграммы начинается с разбиения плоскости на 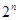 ячеек с помощью
ячеек с помощью 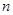 фигур (замкнутых линий), где
фигур (замкнутых линий), где 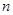 – число различных множеств, участвующих в данной совокупности соотношений.
– число различных множеств, участвующих в данной совокупности соотношений.
При этом каждая последующая фигура должна иметь одну и только одну общую область с каждой из ранее построенных фигур. Такое разбиение называют символом Венна.
На рис. 3 показан символ Венна для 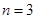 , разбивающий плоскость на 8 ячеек (внешняя область также считается ячейкой). Для определенного количества , разбивающий плоскость на 8 ячеек (внешняя область также считается ячейкой). Для определенного количества 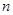 переменных символ Венна имеет стандартный вид. переменных символ Венна имеет стандартный вид.
| 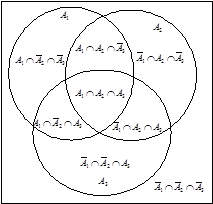
|
| Рис. 3 |
Замкнутые области символа Венна, как и круги Эйлера, соответствуют переменным (множествам 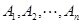 ), а каждая ее область – пересечению
), а каждая ее область – пересечению 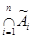 , где символ ~ указывает, что под знаком пересечения стоит соответствующая переменная
, где символ ~ указывает, что под знаком пересечения стоит соответствующая переменная 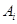 или ее дополнение
или ее дополнение 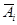 . При этом внешняя область соответствует пересечению дополнений всех переменных
. При этом внешняя область соответствует пересечению дополнений всех переменных 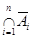 . Универсум отождествляется с плоскостью, которая может ограничиваться замкнутой линией, образующей какую-нибудь фигуру (прямоугольник, круг или овал).
. Универсум отождествляется с плоскостью, которая может ограничиваться замкнутой линией, образующей какую-нибудь фигуру (прямоугольник, круг или овал).
Система теоретико-множественных соотношений отображается на символ Венна выделением (штриховкой) тех ячеек, которые соответствуют пустым подмножествам. В результате получается диаграмму Венна, Объединение любой совокупности заштрихованных ячеек соответствует пустому множеству 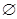 , а объединение всех незаштрихованных ячеек дает универсум
, а объединение всех незаштрихованных ячеек дает универсум 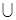 .
.
Для отображения уравнения с правой частью, равной 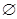 , достаточно заштриховать области, соответствующие левой части уравнения. Уравнение
, достаточно заштриховать области, соответствующие левой части уравнения. Уравнение 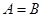 преобразуется в соответствии с формулой (20) (табл. 1) к виду
преобразуется в соответствии с формулой (20) (табл. 1) к виду 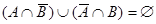 .Это значит, что следует заштриховать все те области в
.Это значит, что следует заштриховать все те области в  , которые не входят в
, которые не входят в  , и те области в
, и те области в  , которые не входят в
, которые не входят в  .
.
Включению 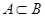 на основании свойства 19 (табл. 1) соответствует уравнение
на основании свойства 19 (табл. 1) соответствует уравнение 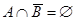 . Его отображение на диаграмме осуществляется штриховкой ячейки, соответствующей пересечению
. Его отображение на диаграмме осуществляется штриховкой ячейки, соответствующей пересечению  с дополнением
с дополнением  .
.
В качестве примера применения диаграмм Венна рассмотрим решение уравнения 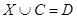 . Его отображение на диаграмму Венна осуществляется штриховкой ячеек в . Его отображение на диаграмму Венна осуществляется штриховкой ячеек в 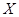 и и 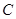 , которые не входят в , которые не входят в 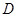 , а также всех ячеек в , а также всех ячеек в 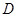 , которые не входят ни в , которые не входят ни в 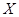 , ни в , ни в 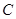 (рис. 4).
Из диаграммы Венна (заштрихованную часть не учитывается) получаем (рис. 4).
Из диаграммы Венна (заштрихованную часть не учитывается) получаем 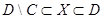 . .
| 
|
| Рис. 4 |
Важно отметить, что этот результат содержится в диаграмме Венна и не требуется никакой дополнительной информации, чтобы судить о свойствах решения уравнения.
Произведение множеств (его также называют декартовым произведением) 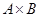 есть множество всех упорядоченных пар элементов
есть множество всех упорядоченных пар элементов 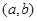 , из которых первый
, из которых первый 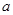 принадлежит множеству
принадлежит множеству  , а второй
, а второй 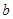 – множеству
– множеству  . Пусть, например,
. Пусть, например, 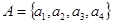 и
и 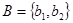 . Тогда
. Тогда
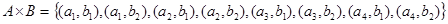 .
.
Порядок следования пар может быть любым, но расположение элементов в каждой паре определяется порядком следования перемножаемых множеств. Поэтому 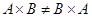 , если
, если 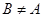 .
.
Операция произведения множеств обобщается на любое их количество 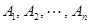 и записывается
и записывается 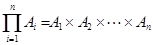 .
.
В результате получаем множество упорядоченных совокупностей элементов ( 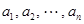 ), которые называются кортежами. Произведение множеств не подчиняется коммутативному и ассоциативному законам, но для него выполняются законы дистрибутивности относительно операций объединения, пересечения и разности:
), которые называются кортежами. Произведение множеств не подчиняется коммутативному и ассоциативному законам, но для него выполняются законы дистрибутивности относительно операций объединения, пересечения и разности:
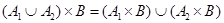 ;
;
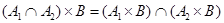 ;
;
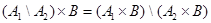 .
.
Для произведения 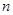 одинаковых множеств
одинаковых множеств  используется обозначение через степень
используется обозначение через степень 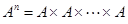 , где
, где  повторяется
повторяется 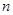 раз. В этом случае кортежи содержат элементы множества
раз. В этом случае кортежи содержат элементы множества  , среди которых могут быть одинаковые элементы. Так, если
, среди которых могут быть одинаковые элементы. Так, если 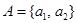 , то
, то
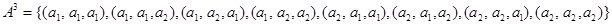 .
.
Следует обратить внимание на существенное отличие операции произведения множеств от операций объединения, пересечения, разности и суммы, в результате выполнения которых всегда получается множество, элементы которого (если оно не пустое) принадлежат исходным множествам. Элементы произведения множеств существенно отличаются от элементов сомножителей и представляют собой объекты другой категории. Пусть 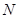 – множество натуральных чисел. Тогда
– множество натуральных чисел. Тогда 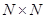 будет множество пар натуральных чисел (
будет множество пар натуральных чисел ( 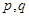 ), каждая из которых определяет самые различные объекты, например: номера домов
), каждая из которых определяет самые различные объекты, например: номера домов 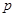 и квартир
и квартир 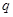 (пара
(пара 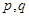 определяет часть адреса), пары участников шахматного турнира в соответствии с жеребьевкой (
определяет часть адреса), пары участников шахматного турнира в соответствии с жеребьевкой ( 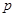 играет белыми,
играет белыми, 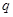 – черными) и т. п. При этом, как указывалось,
– черными) и т. п. При этом, как указывалось, 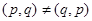 . Если бы это правило не соблюдалось, то номера домов могли бы стать номерами квартир и т. п.
. Если бы это правило не соблюдалось, то номера домов могли бы стать номерами квартир и т. п.
Контрольные вопросы к лекции 1
1-1. Что называется множеством?
1-2. В чем состоит отношение принадлежности?
1-3. Когда два множества тождественны?
1-4. Равны ли между собой множества 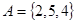 и
и 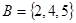 , если нет, то почему?
, если нет, то почему?
1-5. Равны ли между собой множества 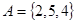 и
и 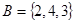 , если нет, то почему?
, если нет, то почему?
1-6. Равны ли между собой множества 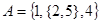 и
и 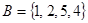 , если нет, то почему?
, если нет, то почему?
1-7. Какое множество называется пустым?
1-8. В чем состоит отношение включения?
1-9. Как определить равенство двух множеств через отношение включения?
1-10. Сколько элементов содержит множество подмножеств множества, содержащего 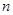 элементов?
элементов?
1-11. Является ли верным соотношение 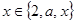 и почему?
и почему?
1-12. Является ли верным соотношение 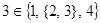 и почему?
и почему?
1-13. Является ли верным соотношение 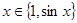 и почему?
и почему?
1-14. Связаны ли множества 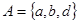 и
и 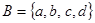 отношением включения? Если да, то укажите, какое из них является подмножеством другого.
отношением включения? Если да, то укажите, какое из них является подмножеством другого.
1-15. Связаны ли множества 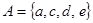 и
и 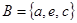 отношением включения? Если да, то укажите, какое из них является подмножеством другого.
отношением включения? Если да, то укажите, какое из них является подмножеством другого.
1-16. Что называется основным множеством?
1-17. Как выполняется операция объединения множеств?
1-18. Как выполняется операция пересечения множеств?
1-19. Как выполняется получение разности множеств?
1-20. Как выполняется получение дизъюнктивной суммы множеств?
1-21. Изобразите с помощью кругов Эйлера выполнение над множествами  и
и  операции
операции 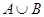 .
.
1-22. Изобразите с помощью кругов Эйлера выполнение над множествами  и
и  операции
операции 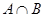 .
.
1-23. Изобразите с помощью кругов Эйлера выполнение над множествами  и
и  операции
операции 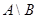 .
.
1-24. Изобразите с помощью кругов Эйлера выполнение над множествами  и
и  операции
операции 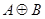 .
.
1-25. Изобразите с помощью кругов Эйлера непересекающиеся множества  и
и  .
.
1-26. Изобразите с помощью кругов Эйлера отношение включения 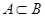 между множествами
между множествами  и
и  .
.
1-27. Изобразите с помощью кругов Эйлера дополнение множества  до универсума.
до универсума.
1-28.Запишите выражение коммутативного закона для объединения множеств.
1-29.Запишите выражение ассоциативного закона для объединения множеств.
1-30.Запишите выражение дистрибутивного закона для объединения множеств.
1-31.Запишите выражение коммутативного закона для пересечения множеств.
1-32.Запишите выражение ассоциативного закона для пересечения множеств.
1-33.Запишите выражение дистрибутивного закона для пересечения множеств.
1-34.Запишите выражения, иллюстрирующие законы Де Моргана.
1-35. Изобразите символ Венна для 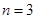 .
.
1-36. Как выполняется операция произведения множеств?
1-37. Что называется кортежем?
1-38. Запишите выражения, иллюстрирующие выполнение для произведения множеств дистрибутивного закона относительно операций объединения, пересечения и разности.
1-39. Что представляет собой операция возведения множества в степень?
1-40. В чем состоит существенное отличие операции произведения множеств от операций объединения, пересечения, разности и суммы?
Дата добавления: 2016-09-06; просмотров: 4706;











