Свойства пересечения и объединения множеств

Из школьного курса математики известно, что операция, при помощи которой находят сумму чисел, называется сложе­нием. Над числами выполняют и другие операции, например умножение, вычитание, деление; при этом результат умноже­ния чисел называют произведением, деления - частным, т.е. для операций над числами и результатов этих операций суще­ствуют разные термины. Для рассмотренных операций над множествами ситуация иная: операции, при помощи которых находят пересечение и объединение множеств, называются соответственно пересечением и объединением.

Из школьного курса математики нам также известно, что операции над числами обладают рядом свойств. Например, сложение действительных чисел обладает переместительным и сочетательным свойствами: для любых действительных чисел а и Ь справедливо равенство а + b = b + а, а для любых чисел a, b и с - равенство (а + b)+ с = а + b+ с).

Аналогичными свойствами обладает умножение действи­тельных чисел. Кроме того, для сложения и умножения выпол­няется распределительное свойство: для любых действительных чисел а, b и с справедливо равенство: (а+b) · с = а · с + b ·с.

Выясним, обладают ли «похожими» свойствами пересече­ние и объединение множеств.

Если обратиться к определениям пересечения и объедине­ния множеств, то можно увидеть, что в них не фиксируется порядок оперирования множествами. Например, выполняя объединение, можно к элементам одного множества присоединить элементы другого, а можно поступить наоборот: к элементам второго множества присоединить элементы перво­го. (При этом надо только помнить, что в новом множестве не должно быть повторяющихся элементов.) Аналогичная си­туация и в случае, когда выполняется пересечение множеств. Это означает, что пересечение и объединение множеств обла­дают переместительным, или, как говорят в математике, ком­мутативным свойством: для любых множеств А и В выпол­няются равенства: А В = В A и A B = B A.

Пересечение и объединение множеств обладают также со­четательным, или ассоциативным, свойством: для любых множеств А, В и С выполняются равенства:

(А В) С = А (В С и (А В) С = А (В С).

Заметим, что назначение скобок в этих записях то же, что и в записях операций над числами.

Свойство ассоциативности для пересечения и объединения множеств не столь очевидно, как свойство коммутативности, и поэтому нуждается в доказательстве. Но прежде можно эти свойства проиллюстрировать при помощи кругов Эйлера. Рассмотрим, например, ассоциативное свойство пересечения множеств. Изобразим множества А, В и С в виде трех попарно пересекающихся кругов (рис. 9).

В выражении (А В) С скобки определяют следующий порядок действий: сначала выполняется пересечение множеств А и В - оно показано на рисунке 9а вертикальной штрихов­кой, а затем находят пересечение полученного множества и множества С. Если выделить множество С горизонтальной штриховкой, то область, заштрихованная дважды, будет изо­бражать множество (А В) С.

Представим теперь наглядно множество А (В С). В соответствии с указанным порядком действий сначала

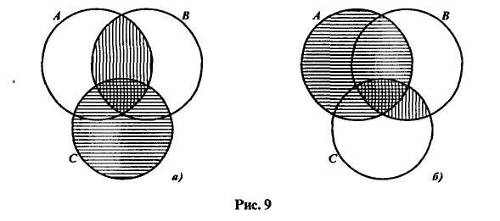
надо найти пересечение множеств В и С - на рисунке 96 оно показано вертикальной штриховкой, а затем выполнить пересечение множества А с полученным множеством. Если отметить множество А горизонтальной штриховкой, то область, заштрихованная дважды, и будет изображать множество А (В С).

Видим, что области, представляющие на рисунке 9 множества (А В) С и А (В С), одинаковы, что и подтверждает справедливость свойства ассоциативности для пересечения множеств.

Аналогично можно проиллюстрировать свойство ассоциативности и для объединения множеств.

В чем важность ассоциативного свойства пересечения и объединения множеств? Во-первых, можно находить пересечение и объединение трех множеств, зная, как это делать для двух. Во-вторых, на основании этого свойства в выражениях А (В С), (А В) С, А (В С), (А В) С можно опускать скобки и писать А В С или А В С, что облегчает запись.

Рассмотрим строгое доказательство свойства ассоциативности одной из операций над множествами, например объединения, т.е. докажем, что для любых множеств А,В и С справедливо равенство (А B) C = А (B С).

Чтобы доказать равенство двух множеств, надо убедиться в том, что каждый элемент множества (А В) С содержится в множестве А (В С), и наоборот.

1. Пусть х - любой элемент множества (А В) С. Тогда, по определению объединения, х А В или х С.

Если х А В, то, по определению объединения, х А или х В. В том случае, когда х А, то, также по определению объединения, х А (В С).

Если х В, то имеем, что х В С, а значит, х А (В С). Случай, когда х А и х В, сводится к рассмотренным. Таким образом, из того, что х А В, следует, что х А (В С).

Если х С, то, по определению объединения, х В С, и следовательно, х А (В С).

Случай, когда х А В и х С, сводится к рассмотренным выше.

Итак, мы показали, что каждый элемент множества (А В) С содержится и в множестве А (В С), т.е. (А В) С А (В С).

2. Пусть y - любой элемент множества А (В С). Тогда, по определению объединения, у А или у В С.

Если y А, то, по определению объединения, у А В и, следовательно, у А и (В С).

Если y В С, то у В или у C. B том случае, когда у В, то у А В и, значит, у (А В) и С. Когда же у С, то у (А B) C. Случай, когда у В и у С, сводится к уже рассмотренным.

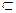Итак, мы показали, что каждый элемент множества А (B С) содержится в множестве (A В) С, т.е. А (В С) (А В) С.

Согласно определению равных множеств заключаем, что (А В) С = А (В С), что и требовалось доказать.

Аналогично доказывается и ассоциативное свойство пересечения множеств.

Взаимосвязь пересечения и объединения множеств отражается в распределительных, или дистрибутивных, свойствах этих операций. Таких свойств два:

1. Пересечение дистрибутивно относительно объединения множеств, т.е. для любых множеств А, В к С выполняется равенство

(А В) С = (А С) (В С).

2. Объединение дистрибутивно относительно пересечения множеств, т.е. для любых множеств А, В и С выполняется равенство

(А В) С = (А С) (В С).

Заметим, что если в выражении есть знаки пересечения и объединения множеств и нет скобок, то сначала выполняют пересечение, так как считают, что пересечение более «сильная» операция, чем объединение. В связи со сказанным запись дистрибутивного свойства пересечения относительно объединения можно упростить, опустив скобки в правой части равенства.

Убедиться в справедливости сформулированных свойств можно путем доказательства, которое аналогично доказательству свойства ассоциативности объединения.

Проиллюстрировать свойства дистрибутивности можно, используя круги Эйлера.

Если провести аналогию с действиями над числами, то можно увидеть, что дистрибутивное свойство пересечения относительно объединения сопоставимо с распределительным свойством умножения относительно сложения, при условии, что в качестве операции, аналогичной пересечению, рассматривать умножение, а для объединения - сложение.

Но для дистрибутивного свойства объединения множеств относительно пересечения аналогичного свойства над числами нет.

Действительно, наличие такого свойства означало бы, что для всех чисел выполняется равенство а • b + с = (а + с) • (b + с), что невозможно. Подмеченное отличие говорит о том, что наряду с тем, что пересечение и объединение множеств обладают рядом свойств, аналогичных свойствам сложения и умножения чисел, операции над множествами обладают свойствами, которых нет у операций над числами.

Завершая рассмотрение свойств пересечения и объединения множеств, отметим еще следующее.

Понятие пересечения и объединения множеств можно обобщить на любое конечное число множеств:

А₁ А₂ ... А_n = {х | х А₁ и х А₂ и... и х А_n},

А₁ А₂ ... А_n = {х | х А₁ или х А₂ или ... или х А_n},

Аналогично можно поступить и по отношению к рассмотренным свойствам данных операций.