Разложение N – мерного вектора
Множество векторов {vk, k=1,2,…N} в N – мерном пространстве, где
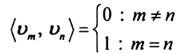
(т.е. vm vn взаимно перпендикулярны и являются единичными), называется ортонормированным базисом.
Если все векторы взаимно перпендикулярны, то ни один из них нельзя выразить через другие векторы. Иначе говоря, они независимы.
Используя ортонормированный базис, можно представить N – мерный вектор в виде линейной комбинации базисных векторов.
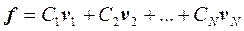
В этой формуле, по аналогии с приведенной ранее, коэффициент Ck выражается как:
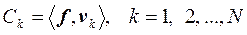
Коэффициент Ck показывает величину составляющей вектора f в направлении вектора vk и выражается в виде скалярного произведения f и vk
Разложение функции
Возникает вопрос, нельзя ли ввести ортонормированную систему в пространство функций так же, как она вводится для векторного пространства? Иначе говоря, нельзя ли ввести множество взаимно перпендикулярных единичных функций? Если это возможно, то  рассматриваемую функцию можно выразить в виде линейной комбинации таких функций. То есть ее можно разложить на составляющие – функции, свойства которых известны заранее.
рассматриваемую функцию можно выразить в виде линейной комбинации таких функций. То есть ее можно разложить на составляющие – функции, свойства которых известны заранее.
Введем ортонормированную систему функций
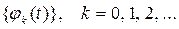 на отрезке [a,b]
на отрезке [a,b]
Условие их ортонормированности:
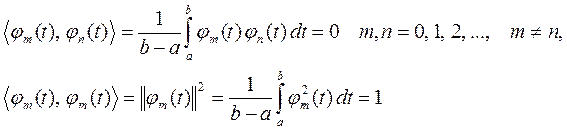
С помощью ортонормированной системы функций функцию f(t) можно выразить следующим образом.
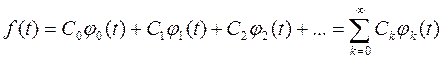
Из этого соотношения понятно, что коэффициент Ck выражает долю составляющей fk(t) функции f(t). Мы уже знаем, что для вывода выражения Ck нужно взять скалярное произведение f(t) и fk(t). Из предыдущих соотношений получим:
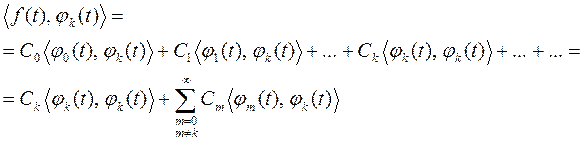
По определению системы ортонормированных функций, скалярное произведение всех комбинаций с 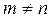 равно нулю, поэтому в итоге в правой части равенства остается лишь Ck. Следовательно,
равно нулю, поэтому в итоге в правой части равенства остается лишь Ck. Следовательно,

Разложение непрерывного сигнала в ряд Фурье на интервале [-π, π]
Возьмем систему функций
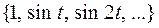
на отрезке 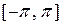 , проверим, является ли она ортонормированной и вычислим коэффициенты разложения Ck. Для того, чтобы исследовать это, нужно проверить являются ли функции разложения попарно ортогональными:
, проверим, является ли она ортонормированной и вычислим коэффициенты разложения Ck. Для того, чтобы исследовать это, нужно проверить являются ли функции разложения попарно ортогональными:
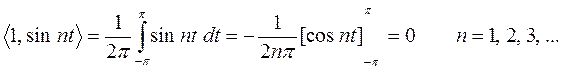
Следовательно, 1 и sin nt ортогональны. Если 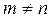 , то
, то
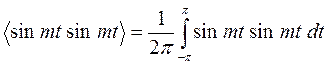
Используя формулу преобразования тригонометрических выражений
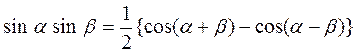
получим:
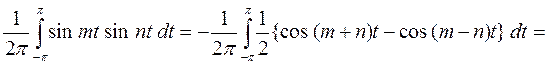
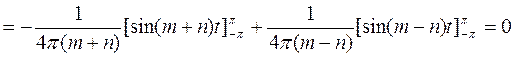
Т.е. sin mt и sin nt ( 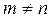 ) также взаимно ортогональны.
) также взаимно ортогональны.
Из вышеизложенных результатов следует, что множество функций {1, sin t, sin 2t, …} образуют систему ортогональных функций. Однако норма каждой функции
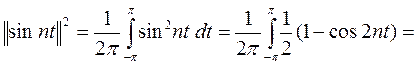
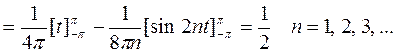
не равна 1, а значит, функции не являются ортонормированными.
Если норма 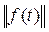 функции f(t) не равна 1, то создадим новую функцию f*(t):
функции f(t) не равна 1, то создадим новую функцию f*(t):
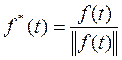
Очевидно, что норма f*(t) равна 1. Подобная операция называется нормировкой системы функций. В нашем случае
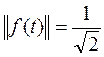
поэтому, представляя исходную систему функций в новом виде:
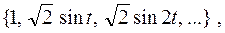
получим множество функций, образующих систему ортонормированных функций. Аналогично можно показать, что ортонормированной является система функций




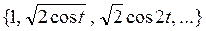
и 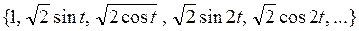 .
.
Таким образом, любую непрерывную функцию f(t) можно разложить в ряд по тригонометрическим функциям (в ряд Фурье):
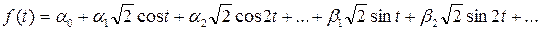
а коэффициенты разложения 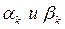 вычислить следующим образом:
вычислить следующим образом:
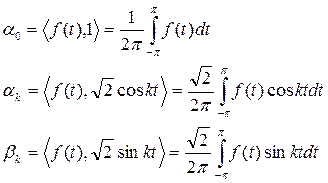
Для упрощения выражения разложения введем замену переменных
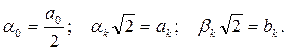

Тогда разложение будет иметь вид:
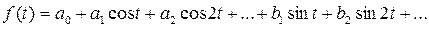
 , (1)
, (1)
где
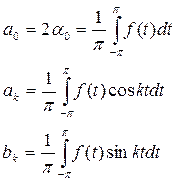
Выражение (1) можно привести к более простому и более информативному виду, где k-я гармоника будет представлена не двумя слагаемыми
akcos(kt) +bksin(kt), (2)
а одним. Для этого представим (2) в виде:
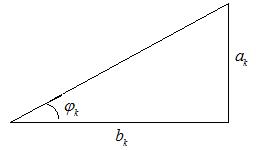
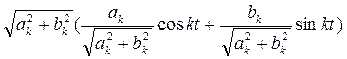
Из геометрической интерпретации рис. 2.3 видно, что величина гипотенузы треугольника равна 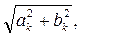 a
a


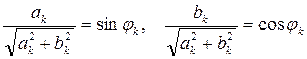
С учетом этого можно записать:
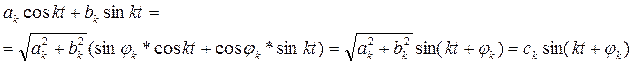
т.к. из формул преобразования тригонометрических выражений
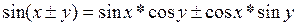 ,
,
а разложение в ряд Фурье запишется как:
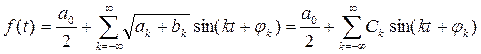 ,
,
где 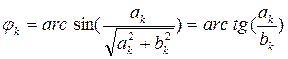 ,
,
 В результате разложение в ряд Фурье будет представлено в виде суммы синусоид с разными фазовыми сдвигами.
В результате разложение в ряд Фурье будет представлено в виде суммы синусоид с разными фазовыми сдвигами.
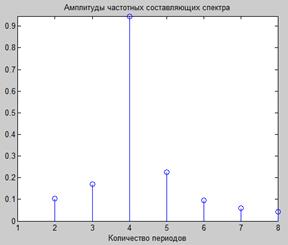
Множество Ck называют спектром амплитуд, множество  – спектром фаз. Множество Ck2 называют спектром мощности.
– спектром фаз. Множество Ck2 называют спектром мощности.
Пример спектра амплитуд дискретизированного гармонического сигнала, содержащего 4.2 периода при использовании 8 членов разложения приведен на рис. 2.4.
Примечание.
1. Не всякую функцию f(t) можно разложить в ряд Фурье. Функция f(t) должна удовлетворять условиям Дирихле.
Функция f(x) на отрезке [a,b] удовлетворяет условиям Дирихле, если:
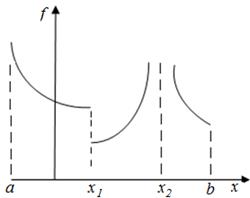
a) f(x) на отрезке [a,b] непрерывна или имеет на этом отрезке конечное число разрывов 1-го рода. Разрыв 1-го рода – это разрыв, при котором существуют пределы функции в данной точке справа и слева. Пример функции f(x), соответствующей условию 1, приведён на рис.2.5.
b) в каждом интервале непрерывности f(x) монотонна[3], либо имеет на этом интервале конечное число точек экстремума. Пример функции f(x), соответствующей условию 2, приведён на рис.2.6.
|
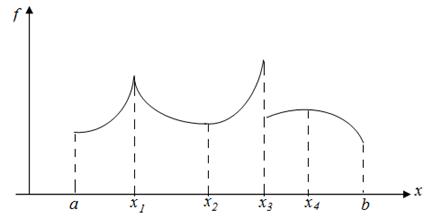
Рис. 2.6.
2. Функции разложения 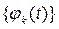 должны удовлетворять не только условиям ортонормированности, но также полноты и замкнутости [9]. Система ортогональных функций
должны удовлетворять не только условиям ортонормированности, но также полноты и замкнутости [9]. Система ортогональных функций 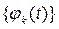 называется замкнутой, если не существует непрерывной функции, не равной тождественно нулю и ортогональной ко всем функциям данной системы. Поэтому из набора замкнутой системы функций разложения
называется замкнутой, если не существует непрерывной функции, не равной тождественно нулю и ортогональной ко всем функциям данной системы. Поэтому из набора замкнутой системы функций разложения
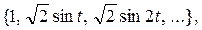
нельзя исключить ни одного элемента, т.к. это нарушило бы условие
замкнутости. Система ортогональных функций 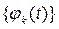 называется полной в промежутке [a,b], если любую непрерывную функцию можно аппроксимировать в среднем с любой степенью точности при помощи линейной комбинации функций
называется полной в промежутке [a,b], если любую непрерывную функцию можно аппроксимировать в среднем с любой степенью точности при помощи линейной комбинации функций 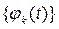 [8]. Иными словами, какого бы ни было
[8]. Иными словами, какого бы ни было 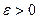 , всегда можно указать такое n в линейной комбинации функций:
, всегда можно указать такое n в линейной комбинации функций:
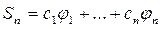 ,
,
что
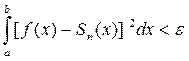
Для полной системы функций 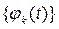 имеет место соотношение
имеет место соотношение
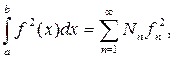
где fn – коэффициенты Фурье функции f(x):
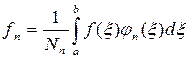
Условиям полноты и замкнутости удовлетворяют не только тригонометрические функции sin(kt) и cos(kt), но и ортогональные полиномы Лежандра, Лагерра, Якоби [8].
Разложение сигнала на систему ортогональных полиномов применяется в математической физике и квантовой механике с целью физической интерпретации происходящих сложных явлений как композиции более простых.
Разложение функции на интервале [-T/2,T/2]
До этого момента мы рассматривали функцию переменной t на отрезке [-p,p]. В случае периодического сигнала с периодом 2p мы брали этот интервал за основной. В общем случае периодического сигнала с периодом Т при разложении в ряд Фурье мы должны использовать интервал [-Т/2, Т/2]. Если интервал [-p,p] расширить (или сократить) до интервала [-T/2, Т/2], то и период первой гармоники увеличится (или уменьшится) от 2 p до Т. Поскольку кратность этого преобразования равна (Т/2)p, то составляющие первой гармоники примут вид:
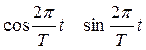
Для составляющих k-й гармоники можно записать:
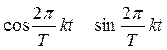
Следовательно, если функцию f(t) разложить в ряд Фурье на интервале [-Т/2, Т/2], получим:
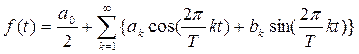
Если обозначить угловую частоту через 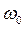 , то поскольку
, то поскольку 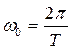 , последнее выражение можно записать и в таком виде:
, последнее выражение можно записать и в таком виде:
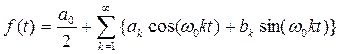
В соотношении, определяющем коэффициенты Фурье на отрезке 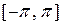
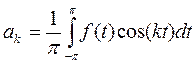
произведем замену переменной 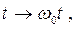
а также замену отрезка, на котором берется интеграл 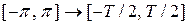
Оставив функцию f(t) без изменения, получим
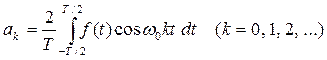
Аналогичным образом выводится следующее соотношение:
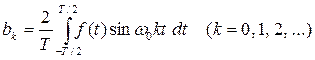
Дата добавления: 2017-01-16; просмотров: 2432;











