Примеры пространств сигналов
Пространство 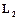
Элементами множества 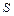 являются в общем случае комплексные функции
являются в общем случае комплексные функции 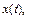 заданные на интервале
заданные на интервале 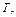 конечном или бесконечном. Будем считать, что функции
конечном или бесконечном. Будем считать, что функции 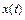 являются функциями с интегрируемым квадратом
являются функциями с интегрируемым квадратом
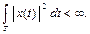
Этот интеграл обычно трактуется как энергия сигнала, если принять, что 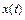 - это ток или напряжение на сопротивлении
- это ток или напряжение на сопротивлении 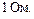
При этом 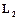 является пространством с ограниченной энергией. Все физические сигналы имеют конечную энергию.
является пространством с ограниченной энергией. Все физические сигналы имеют конечную энергию.
В 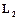 скалярное произведение, норма и расстояние определяются соответственно:
скалярное произведение, норма и расстояние определяются соответственно:
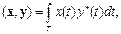
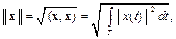
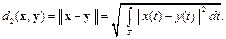
Метрика 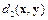 называется среднеквадратичной метрикой и определяет среднеквадратичное отклонение сигнала
называется среднеквадратичной метрикой и определяет среднеквадратичное отклонение сигнала 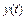 от
от 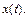
Условие ортогональности двух векторов 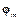 и
и 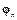 в
в 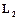 записывается в виде
записывается в виде
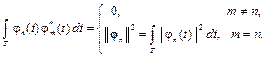
Обобщенный ряд Фурье (1.2.13) в 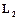 принимает вид
принимает вид
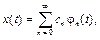
где
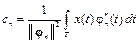
есть коэффициенты Фурье по системе {jn}.
Пространство 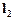
Элементами множества 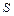 являются последовательности чисел (в общем случае комплексные)
являются последовательности чисел (в общем случае комплексные) 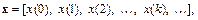 удовлетворяющие условию
удовлетворяющие условию
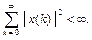
Такие последовательности называют также счётномерными векторами. В данном классе последовательностей вводят операции сложения векторов и умножения их на скаляр:

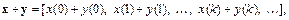
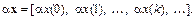
Скалярное произведение, норма и расстояние определяются соответственно
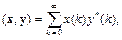
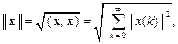
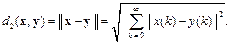
Эти соотношения определяют пространство 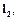 которое можно рассматривать как координатную реализацию гильбертова пространства
которое можно рассматривать как координатную реализацию гильбертова пространства 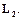
Обратимся к формулам обобщенного ряда Фурье (1.2.13) – (1.2.16). Эти формулы устанавливают взаимно однозначное соответствие (изоморфизм) между сигналом и совокупностью его коэффициентов Фурье. Сигнал 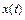 является элементом пространства
является элементом пространства 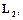 а совокупность коэффициентов Фурье (счетномерный вектор) – элементом пространства
а совокупность коэффициентов Фурье (счетномерный вектор) – элементом пространства 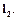 Между пространствами
Между пространствами 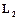 и
и 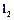 устанавливается изометрия, при которой сохраняется норма элементов пространств
устанавливается изометрия, при которой сохраняется норма элементов пространств 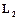 и
и 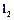 (1.2.18).
(1.2.18).
Пространство 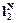
Ограничение размерности векторов до 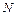 координат
координат 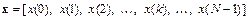 приводит к пространству
приводит к пространству 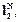 которое является подпространством комплексного гильбертова пространства
которое является подпространством комплексного гильбертова пространства 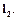 Характерно, что в
Характерно, что в 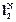 существуют
существуют 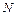 линейно независимых векторов
линейно независимых векторов 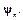 Эти
Эти 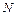 векторов называют базисом N-мерного пространства.
векторов называют базисом N-мерного пространства.
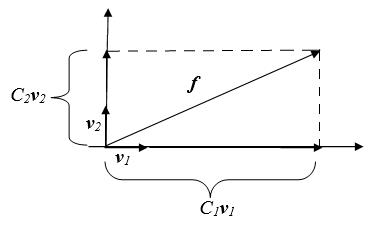 Разложение двумерного вектора
Разложение двумерного вектора
Возможность представления двумерного вектора через проекции на оси координат известно из геометрии и не требует доказательства. Каждую из проекций выражают через единичные вектора v1иv2.
f = C1v1+C2v2 (2.1)
 Однозначное представление будет в том случае, если вектора v1иv2взаимно перпендикулярны(рис.2.2).
Однозначное представление будет в том случае, если вектора v1иv2взаимно перпендикулярны(рис.2.2).
Пара взаимно перпендикулярных векторов {v1,v2} называется ортогональным базисом, а если ||v1||=||v2||=1, то эта пара называется ортонормированным базисом. Вектор с нормой, равной 1, называется единичным вектором. Векторы C1v1 и C2v2 называются проекциями вектора f .
Пусть дан вектор f исистема базисных векторов {v1,v2}. Покажем, чтокоэффициенты С1 и С2 вычисляются как скалярные произведения вектора f на каждый из векторов v1 и v2 .
Найдем скалярное произведение левой и правой частей равенства (2.1) и вектора v1
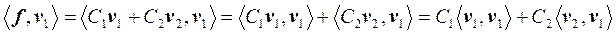
Согласно свойствам базиса
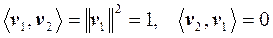
Так как правая часть равна С1, то справедливо равенство:
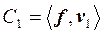
Подобным образом можно получить выражение для С2:
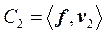
Дата добавления: 2017-01-16; просмотров: 2255;











