РАЗЛОЖЕНИЕ ДИСКРЕТИЗИРОВАННЫХ СИГНАЛОВ В ДЕЙСТВИТЕЛЬНЫЙ РЯД ФУРЬЕ
Разложение функции, представленной в дискретизированном виде, в ряд Фурье на интервале 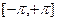
В дискретизированном виде (т.е. в виде набора дискретных значений или, что то же, в виде числового массива, содержащего N значений) функция f(t) на интервале 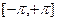 будет иметь вид:
будет иметь вид:
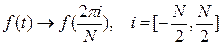
где N – количество дискретных значений сигнала. При 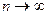 дискретизированная функция будет приближаться к непрерывной f(t).
дискретизированная функция будет приближаться к непрерывной f(t).
Разложение в ряд Фурье будет иметь вид, аналогичный тому, который был получен для случая непрерывного сигнала:
а коэффициенты 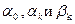 :
:
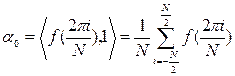 ;
;
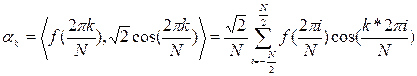 ;
;
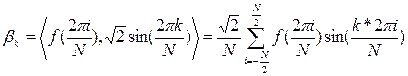 .
.
и коэффициенты a0, ak и bk:
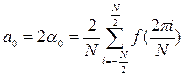
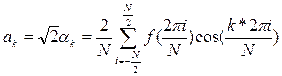
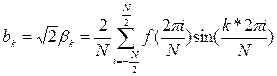
а общий вид разложения:
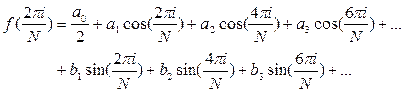
Ниже приведена программа генерации модельного дискретизированного сигнала и вычисления коэффициентов разложения для функций f(t)=sin(t) и f(t)=tp на интервале  .
.
Здесь N-количество элементов массива, K – количество членов ряда Фурье, kp – количество периодов гармонического модельного сигнала, T - диапазон изменения функции f(t).
.
for i=1:N+1
f(i)=sin(2*pi*kp*(i-1)/N); % гармоническая функция
% f(i)= (2*T*(((i-1-N/2))/N))^p; %функция t^p
Sa0=Sa0+f(i);
end
Sa0=Sa0/N
for i=1:N+1
for j=1:K
Sa(j) = (Sa(j)+f(i)*cos((j)*2*pi*(i-1-N/2)/N));
Sb(j) = (Sb(j)+f(i)*sin((j)*2*pi*(i-1-N/2)/N));
end
end
for j=1:K
Sa(j)=Sa(j)*(1/(N/2));
Sb(j)=Sb(j)*(1/(N/2));
end
Обратное дискретное преобразование Фурье выполняется с помощью следующего фрагмента программы.
for i=1:N+1
for j=1:K
y(i)= y(i)+Sa(j)*cos(j*2*pi*(i-1-N/2)/N)+Sb(j)*sin(j*2*pi*(i-1-N/2)/N);
end
y(i)=Sa0+y(i);
end
Примечание. Для разложения четной функции из ряда можно исключить члены, содержащие синусы, для разложения нечетной – косинусы. Но можно оставить ряд разложения полностью.
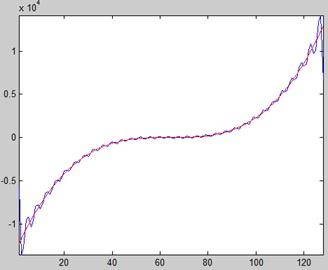
Рис. 3.1. Исходная и восстановленная функция t3 при N=128, K=32,p=3.
Сравнение исходной и восстановленной с помощью обратного преобразования Фурье функции позволяет оценить погрешность, связанную с представлением функции рядом Фурье с конечным числом членов.
Разложение функции, представленной в дискретизированном виде, в ряд Фурье на интервале [-T,T]
В дискретизированном виде (т.е. в виде набора дискретных значений или, что то же, в виде числового массива, содержащего N значений) функция f(t) на интервале [-T,T] будет иметь вид:
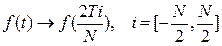
где N – количество дискретных значений сигнала. При 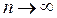 дискретизированная функция будет приближаться к непрерывной f(t).
дискретизированная функция будет приближаться к непрерывной f(t).
Разложение в ряд Фурье будет иметь тот же вид, что и при разложении функции в непрерывной форме, а коэффициенты 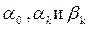 :
:
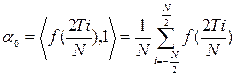 ;
;
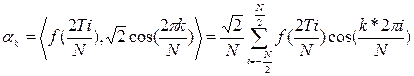 ;
;
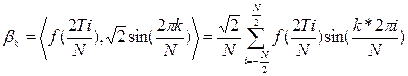 .
.
и коэффициенты a0, ak и bk:
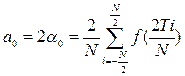
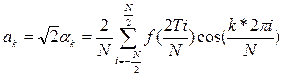
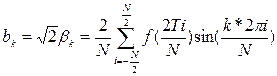
а общий вид разложения:
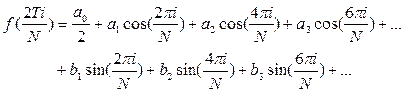
Ниже приведена программа вычисления коэффициентов разложения для функций f(t)=sin(t) и f(t)=tp в дискретизированном виде на интервале [0,T].
Sa0=0;
for i=1:N+1
f(i)=sin(2*pi*kp*(i-1)/N); % гармоническая функция
% f(i)= (T*(((i-1))/N))^p; %функция t^p, i-1, если p>0, i, если p<0
Sa0=Sa0+f(i);
end
Sa0=Sa0/N
for i=1:N+1
for j=1:K
Sa(j) = (Sa(j)+f(i)*cos((j)*2*pi*(i-1)/N));
Sb(j) = (Sb(j)+f(i)*sin((j)*2*pi*(i-1)/N));
end
end
for j=1:K
Sa(j)=Sa(j)*(1/(N/2));
Sb(j)=Sb(j)*(1/(N/2));
end
Примечание.
В ряд Фурье может разлагаться и произвольная непериодическая функция, заданная (ограниченная, вырезанная из другого сигнала, и т.п.) на интервале [a,b], если нас не интересует ее поведение за пределами данного интервала. Однако следует помнить, что применение формул разложения автоматически означает периодическое продолжение данной функции за пределами заданного интервала (в обе стороны от него) с периодом Т = b-a. При этом на краях интервала может возникнуть явление Гиббса, если уровень сигнала на краях не совпадает и образуются скачки сигнала при его периодическом повторении, как это видно на рис. 3.2. При разложении исходной функции в ограниченный ряд Фурье и его обработке в частотной области на самом деле при этом обрабатывается не исходная функция, а реконструированная из ограниченного ряда Фурье[4].
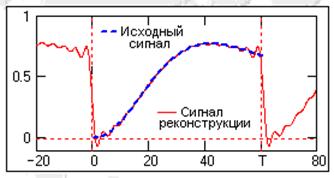
Рис. 3.2. Реконструкция сигнала, ограниченного во времени, с помощью ограниченного ряда Фурье
При усечении рядов Фурье определенное искажение функций существует всегда. Но при малой доле энергии отсекаемой части сигнала (при быстром затухании спектров функций) этот эффект может быть и мало заметен. На скачках и разрывах функций он проявляется наиболее ярко.
Параметры эффекта Гиббса. Большинство методов анализа и обработки сигналов представляют собой или имеют в своем составе операцию свертки сигналов с функцией оператора свертки. Как сигнал, так и оператор свертки, выполняющий определенную задачу обработки данных и реализующий определенную частотную функцию системы обработки, могут быть бесконечно большими. Практика же обработки на ЭВМ может иметь дело только с ограниченными множествами и данных, и коэффициентов оператора. В общем случае, эти ограниченные множества "вырезаются" из бесконечных множеств, а разложение в ряды Фурье, также ограниченные по размерам, является одной из самых распространенных операций обработки цифровых множеств. С учетом этого рассмотрим явление Гиббса более подробно, т.к. при любых ограничениях рядов Фурье оно всегда может весьма существенно сказаться на качестве и точности обработки сигналов.
Очевидно, что при усечении ряда Фурье любой функции до конечного числа членов N мы будем иметь усеченный ряд Фурье:
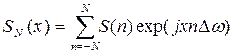

при этом происходит усечение спектральной характеристики функции до частоты nDw и сходимость суммы остающихся членов ряда sN(x) к исходной функции s(x) ухудшается в тем большей степени, чем меньше значение N. Особенно ярко это проявляется на крутых перепадах (разрывах, скачках) функций:
- крутизна перепадов "размывается", т.к. она не может быть больше, чем крутизна (в нулевой точке) последней сохраненной гармоники ряда;
- по обе стороны "размытых" перепадов появляются выбросы и затухающие осцилляции с частотой, равной частоте последнего сохраненного или первого отброшенного члена ряда.
Рассмотрим явление Гиббса на примере разложения в ряд Фурье функции единичного скачка s(x), которая имеет разрыв величиной 1 в точке х = 0 (см. рис. 3.3).
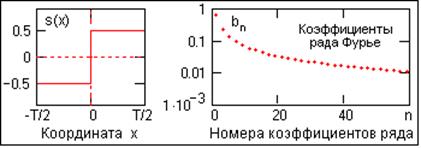
Рис. 3.3.
Уравнение функции:
s(x) = -0.5 при –T/2 ≤ x<0; s(x) = 0.5 при 0 £ x ≤ T/2.
Поскольку функция является нечетной, ее ряд Фурье не содержит косинусных членов, и коэффициенты ряда в односторонней тригонометрической форме определяются выражением (с учетом соотношения Dw = 2p/T):
bn = (2/T) 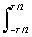 s(x) sin(xnDw) dx = (2/T)
s(x) sin(xnDw) dx = (2/T)  sin(xnDw) dx.
sin(xnDw) dx.
bn = 2/(n·p), n- нечетное,
bn = 0, n- четное.
Реконструкция скачка при трех значениях ряда приведена на рис. 3.4. Как и положено, функция продолжается периодически за пределами заданного интервала (-Т/2, Т/2), при этом на границах периодов также образуются скачки. Скачки являются центрами возникающих осцилляций. Наложение осцилляций друг на друга в зависимости от расстояния между их центрами может как уменьшать амплитуду пульсаций, так и увеличивать.
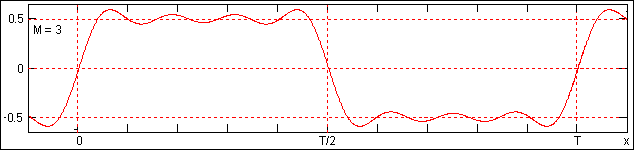
Рис. 3.4. Реконструкция скачка по ограниченному раду Фурье при М=3.
Таким образом, для усеченных рядов Фурье предельные значения максимальных выбросов по обе стороны от скачка и следующих за ними обратных выбросов при единичной амплитуде разрыва функции достигают соответственно 9% и 5% значения амплитуды скачка. Кроме того, сам скачок функции из собственно скачка преобразуется в переходную зону, длина которой между точками максимальных выбросов по обе стороны скачка равна T/(2(M+1)), а по уровню исходных значений функции на скачке (в данном случае от -0.5 до 0.5) порядка (2/3)T/(2(M+1)). Это явление типично для всех функций с разрывами.
Дата добавления: 2017-01-16; просмотров: 3921;











