Гильбертово пространство

Это пространство определяют следующим образом.

1. Задано линейное пространство H

2. Для каждой пары x и y сигналов из H вводится линейная операция <x, y>, называемая скалярным произведением двух векторов, в результате которой образуется скаляр, а не вектор. Эта операция должна удовлетворять аксиомам:

< x, y > = < y, x >*

< x, y+z >=< x, y >+< x, z > (2.9)

< ax, y >=a< x, y >, но < x, ay >=a*< x, y >

<x, x> ≥ 0,

причём <x, x> = 0 тогда и только тогда, когда x=0 Здесь и далее звездочка означает комплексное сопряжение.

3. В H существует счётное число линейно независимых векторов.

Норма или длина вектора определяется как

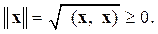(2.10)

В гильбертовом пространстве вводится угол q между двумя векторами, косинус которого определяется через скалярное произведение:

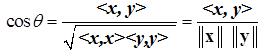(2.11)

Это соотношение используется для определения понятия ортогональных векторов. Векторы x и y называются ортогональными, если их скалярное произведение равно нулю, т. е. если < x, y > =0. Поскольку 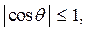то

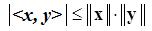(2.12)

– неравенство Коши–Буняковского.

По определению гильбертова пространства в нем существует счетная система линейно независимых векторов, которые можно ортогонализировать, пользуясь известной процедурой Грама–Шмидта[2] [9]. Поэтому в гильбертовом пространстве существует счётная ортогональная система векторов 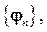образующих ортогональный базис. В этом случае любой вектор 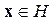может быть представлен в виде

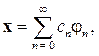(2.13)

где

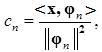(2.14)

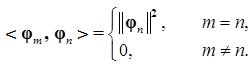(2.15)

Для ортонормированного базиса

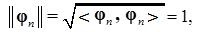(2.16)

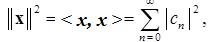(2.17)

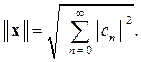(2.18)

Квадрат нормы (2.17) называется энергией сигнала. Ряд (2.13) называется рядом Фурье по базису 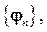а коэффициенты c_n 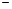коэффициентами Фурье сигнального вектора xв этом базисе.

Аналогично для любых двух векторов x и y имеющих в ортонормированном базисе 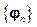спектры {a_n} и {b_n} соответственно, справедливо равенство

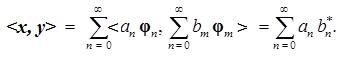(2.19)

При переходе к другому ортонормированному базису координаты a_n и b_n изменятся (станут 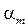и 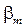соответственно), однако скалярное произведение останется без изменения:

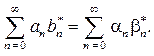(2.20)

Это соотношение называется равенством Парсеваля.

За расстояние между векторами x и y в гильбертовом пространстве принимается длина разностного вектора:

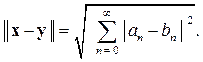(2.21)

Сигналы, принадлежащие гильбертову пространству, изображаются точками и векторами, идущими из начала координат в данную точку. Их можно складывать и умножать на числа. Можно рассматривать длину вектора, представляющего сигнал как его норму, измерять расстояние между сигналами, вводить угол между векторами, изображающими сигналы.

Используем далее представление сигнала в виде вектора, имеющего бесконечную размерность, для исследования возможности представления произвольной функции в виде ряда:

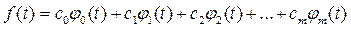
Общеизвестна возможность разложения функций в ряд Фурье. Это позволяет представить функцию (сигнал) в виде совокупности частотных составляющих, т.е. получить частотный спектр сигнала, который может содержать полезную информацию.

Для обнаружения информативных параметров сигнала в ряде случаев, в частности, при анализе полей температуры, давления, профилей сейсмических трасс может быть полезно разложение (декомпозиция) сигналов и по другим (не гармоническим) функциям, например, по полиномам Лежандра, Лагерра.

Для исследования возможности представления произвольной функции в виде ряда рассмотрим разложение двумерного вектора f, затем распространим этот принцип на разложение многомерного вектора и, далее, на разложение вектора бесконечной размерности.