Метрические пространства
Сигналы, обладающие некоторым общим свойством, можно объединить в одно множество S. Примером является множество периодических сигналов, множество сигналов с финитным спектром[1] и т. д. Определив множество, мы начинаем интересоваться отличительными свойствами элементов этого множества. Общий подход заключается в том, что каждой паре элементов 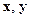 ставится в соответствие действительное положительное число
ставится в соответствие действительное положительное число 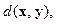 которое трактуется как расстояние между элементами xиy.
которое трактуется как расстояние между элементами xиy.
Множество, в котором определено расстояние, представляет собой пространство сигналов. При этом сигналы удобно рассматривать как векторы в этом пространстве. Функционал 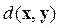 отображает каждую пару элементов на действительную ось и называется метрикой, обладающей следующими свойствами:
отображает каждую пару элементов на действительную ось и называется метрикой, обладающей следующими свойствами:
а) 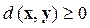 и
и 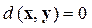 ,если только x=y
,если только x=y
б) 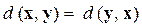 (симметрия);
(симметрия);
в) 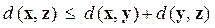 (неравенство треугольника).
(неравенство треугольника).
Множество S с метрикой d называется метрическим пространством. Две разные метрики, определённые на одном и том же множестве, порождают разные метрические пространства. Приведём примеры часто используемых метрик.
Для аналоговых сигналов, заданных на интервале [0, T]
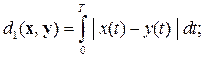 (2.1)
(2.1)
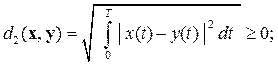 (2.2)
(2.2)
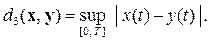 (2.3)
(2.3)
Для дискретных сигналов, заданных на интервале 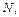
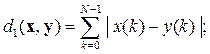 (2.4)
(2.4)
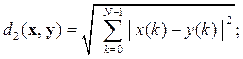 (2.5)
(2.5)
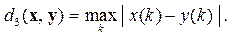 (2.6)
(2.6)
В пространстве n-разрядных двоичных сигналов расстояние между любой парой таких сигналов
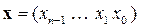 и
и 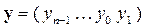
вполне будет определяться числом несовпадающих символов:
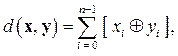 (2.7)
(2.7)
где Å означает сложение по модулю 2: 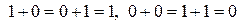 без переноса в старший разряд. Метрика (2.7) определяет расстояние по Хеммингу для двоичных слов.
без переноса в старший разряд. Метрика (2.7) определяет расстояние по Хеммингу для двоичных слов.
Дата добавления: 2017-01-16; просмотров: 2138;











