Базис пространства и координаты вектора

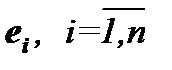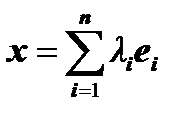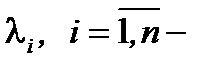Рассмотрим векторы . Вектор , где некоторые числа, называется линейной комбинацией векторов 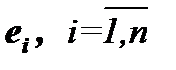. Векторы 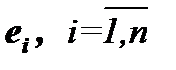называютя линейно зависимыми, если существуют такие постоянные числа 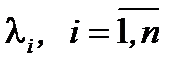не все одновременно равные нулю, что выполняется равенство

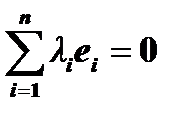. (3)

Если же равенство (3) выполняется только 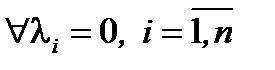, то векторы 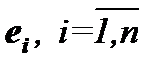называются линейно независимыми. Заметим, два вектора линейно зависимы тогда и только тогда, когда они коллинеарны; три вектора линейно зависимы тогда и только тогда, когда они компланарны; четыре вектора всегда линейно зависимы.

Множество векторов называется векторным пространством, если линейная комбинация любых векторов множества также является вектором этого множества. Векторными пространствами являются, например, множество коллинеарных векторов, множество компланарных векторов, множество векторов обычного пространства. Упомянутые выше векторные пространства обозначаются соответственно через .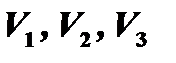

Пусть 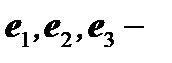линейно независимые векторы пространства 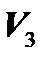. Можно доказать, что любой вектор 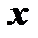пространства 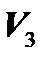однозначно представим в виде линейной комбинации трех линейно независимых векторов 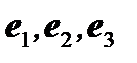этого пространства, т.е.

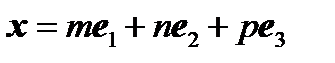(4)

Всякая совокупность линейно независимых векторов, через которые линейно выражается любой вектор пространства, называется базисом этого пространства. Векторы, составляющие базис пространства, называются базисными. Таким образом, выражение (4) представляет собой разложение произвольного вектора 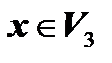по базису 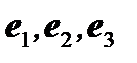. Коэффициенты m, n, p в разложении называются координатами вектора 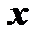в этом базисе. Всякий вектор 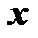, имеющий своими координатами в некотором базисе числа m, n, p, будем записывать в виде

.

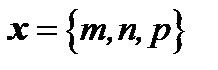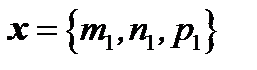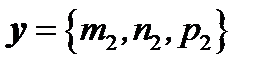Если и , то , .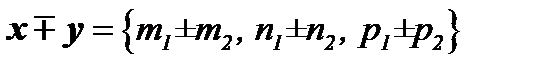

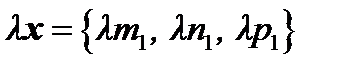Базис, состоящий из взаимно перпендикулярных единичных векторов, называется ортонормированным. Векторы ортонормированного базиса называются ортами и обозначаются через 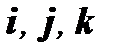. Таким образом, в ортонормированном базисе разложение вектора имеет вид

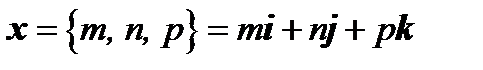
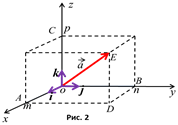
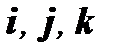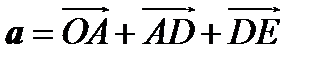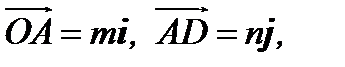
Выберем декартову прямоугольную систему координат и обозначим символами орты координатных осей 0x, 0y и 0z соответственно. Из рис.2 имеем , , 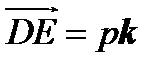следовательно, 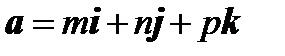. Известно, что квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его измерений, следовательно

.

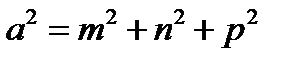Откуда 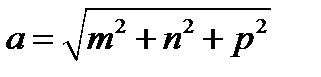. Но 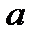есть длина вектора 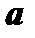. Таким образом длина вектора 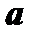, координаты которого 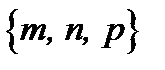вычисляется по формуле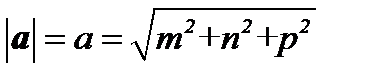

Обозначим через 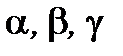углы, образованные данным вектором 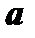с координатными осями 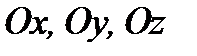соответственно. Условимся при этом углы отсчитывать от положительных координатных полуосей. Тогда каждый из этих углов будет принадлежать промежутку 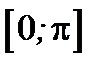Углы эти однозначно определяют направление вектора; косинусы этих углов называют направляющими косинусами вектора. Т.к. 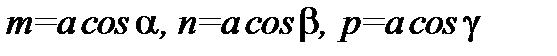, то

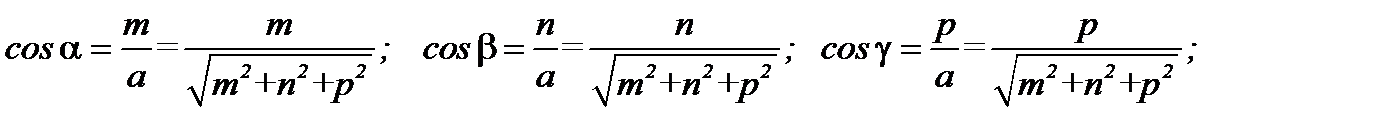
Вектор, координаты которого 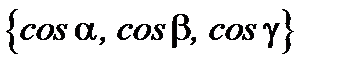называется единичным вектором вектора и записывается

.

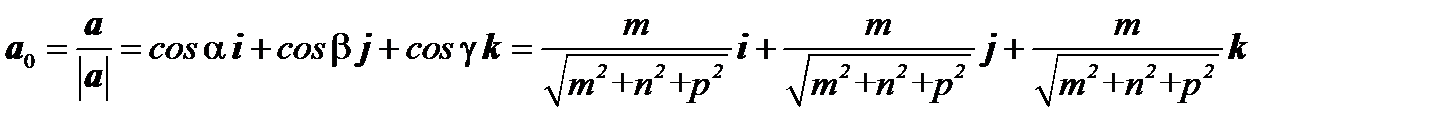Заметим .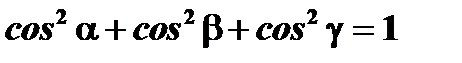

Пусть даны два вектора, разложенные по базису :

.

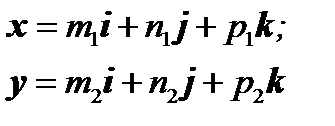Два вектора коллинеарны тогда и только тогда, когда они линейно зависимы, т.е.

,

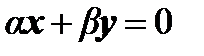Где хотя бы одно из чисел 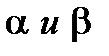отличны от нуля. Пусть для определенности 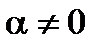. Тогда 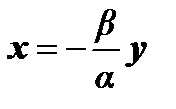, откуда 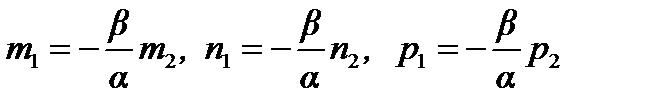или

.

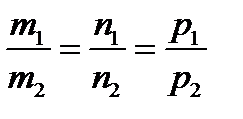Следовательно, необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их координат в данном базисе:

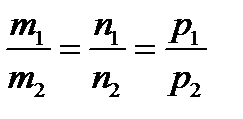( 5)