Вектора по базису пространства

ЛинейнОе пространство

1.1. Определения. Базис и размерность. Разложение

вектора по базису пространства

ОПРЕДЕЛЕНИЕ 1. Множество L называется линейным, если для элементов этого множества выполнены следующие условия:

а) в L введено сложение элементов, то есть 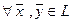введено отображение

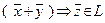, (1)

обладающее следующими свойствами:

,

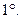
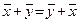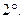
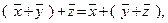
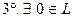такой, что ,

,

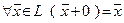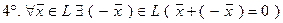(элемент - 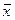называется противоположным элементу );

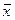б) в множестве L введена операция умножения элементов на действительные числа, то есть 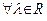и 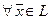определено отображение

,

обладающее свойствами:

,

,

,

.

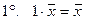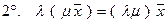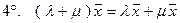Следует отметить, что элементами линейного пространства , как правило, являются векторы.

ОПРЕДЕЛЕНИЕ 2. Пространство L называется действительным, если в L операция умножения векторов на число определена только для действительных чисел, и - комплексным, если эта операция определена для комплексных чисел.

ОПРЕДЕЛЕНИЕ 3. Система векторов называется линейнозависимой, если найдутся такие числа 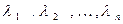, что

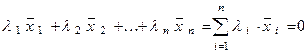, (2)

причем

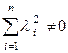, (3)

и эта система векторов называется линейно независимой, если

(4)

Условие 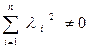означает, что среди всех 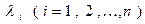существует хотя бы одно число не равное нулю.

Т е о р е м а 1. Если система векторов 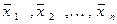является линейно зависимой, то один из векторов этой системы является линейной комбинацией остальных.

Д о к а з а т е л ь с т в о. Запишем условие линейной зависимости векторов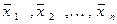

. (5)

Пусть для определенности 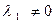, тогда из (5) имеем:

.

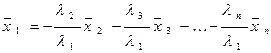Таким образом, вектор 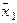является линейной комбинацией остальных векторов.