Вектори, лінійні операції над векторами

Означення. Вектором називається напрямлений відрізок. Позначати вектори будемо 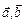, ... . Якщо, скажімо, точка А — початок вектора, а точка В — його кінець, то маємо .

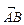Вектор, в якого початок і кінець збігаються, називається нульовим вектором.

Вектор вважається заданим, коли відома його довжина 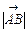, 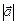і напрям щодо деякої осі.

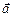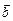Два вектори і називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих.

Вектори 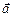і 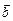вважаються рівними, коли вони: 1) колінеарні; 2) однаково напрямлені; 3) їхні довжини рівні.

З останнього випливає, що при паралельному перенесенні вектора дістаємо новий вектор, що дорівнює попередньому, тому вектори в аналітичній геометрії називають вільними.

Нехай у просторі задано деяку вісь l і вектор 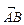. Проведемо через точки А і В площини, перпендикулярно до осі l (рис. 2.7). Позначимо точки перетину цих площин з віссю l відповідно 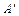і .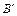

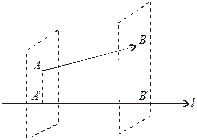Рис. 3.1

Означення. Проекцією вектора 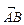на вісь l називається довжина 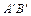напрямленого відрізка 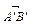на осі l. Слід зазначити, що 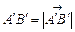, якщо напрям 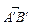збігається з напрямом l і 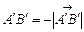, якщо напрям 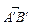протилежний напряму l.

Позначається проекція вектора 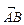на вісь l — пр_l 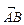. З рис. 2.7 випливає формула знаходження проекції вектора на вісь:

пр_l = ,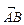

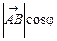де 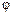— кут між вектором і віссю.

Якщо розглянути прямокутну декартову систему координат і точки початку А (х₁, у₁, z₁) і кінця В (х₂, у₂, z₂) вектора 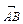, то проекції вектора 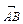на кожну з осей мають вигляд:

Ох: а_х = х₂ – х₁, Оу: а_у = у₂ – у₁, Оz: а_z = z₂ – z₁.

Довжина вектора подається формулою:

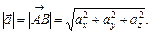(3.1)

Якщо позначити a, b, g — кути між вектором 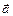і відповідними осями системи координат, то їх косинуси можна знайти за формулами:

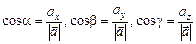. (3.2)

У подальшому називатимемо їх напрямними косинусами вектора 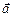. Піднісши кожну з формул (2.5) до квадрата і скориставшись (2.4), дістанемо:

cos²a + cos²b + cos²g = 1.

Дії з векторами виконуються за правилами:

1. Додавання:

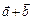= (а_х + b_х, а_у + b_у, а_z + b_z).

2. Множення вектора на число a Î R:

.

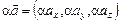Для лінійних операцій з векторами виконуються властивості:

1. .

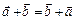2. .

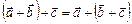3. .

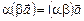4. .

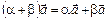5. .

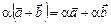Теорема. Проекція суми двох векторів на вісь дорівнює сумі їхніх проекцій на цю вісь:

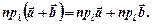
Теорема. При множенні вектора на число його проекція на цю вісь також множиться на це число:

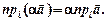
Нехай вектори 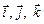такі, що за напрямом збігаються відпо-
відно з осями Ох, Оу, Оz і 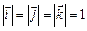. Такі вектори надалі називатимемо одиничними векторами осей системи координат. Тоді

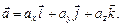(3.3)