РАЗЛОЖЕНИЕ ФУНКЦИЙ В КОМПЛЕКСНЫЙ РЯД ФУРЬЕ

Система функций 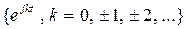на отрезке 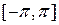образует ортонормированную систему функций. Значит, произвольная функция f(t) может быть представлена по этой системе следующим образом:

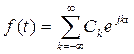
Коэффициенты С_k называются комплексными коэффициентами Фурье и, подобно действительным коэффициентам Фурье, вычисляются как скалярные произведения f(t) и e^jkt:

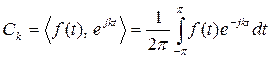
Если период функции не равен 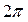, а, например, равен Т, то получим следующее общее выражение для комплексных коэффициентов:

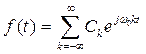
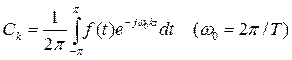
Коэффициенты Фурье являются комплексными числами, но f(t) является действительной функцией, а значит правая часть последнего выражения должна быть действительной. Так оно и есть на самом деле, потому что коэффициенты C_k и C-k являются сопряженными. Если взяты целые положительные значения k, то функцию f(t) можно записать в виде:

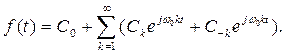
Но, учитывая то, что C_k и C-k являются сопряжёнными, получим:

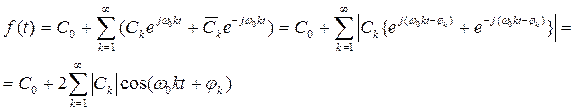
В дискретизированном виде разложение функции, представленной N значениями, в комплексный ряд Фурье, содержащий k элементов разложения, будет иметь вид:

,

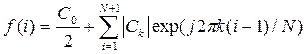а коэффициенты C₀…C_k вычислятся по формулам:

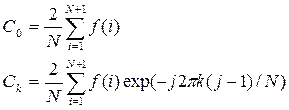
Ниже приведена программа разложения дискретизированной функции f(t)=t² содержащего N значений в комплексный ряд Фурье на интервале [-T,T] с М членами разложения, M<N, и последующего восстановления. Для сравнения приведены результаты, полученные с помощью стандартных функций fft (БПФ) и ifft (ОБПФ) MATLAB.

for i=1:N+1 %генерация модельной функции

f(i)=sin(2*pi*kp*(i-1)/N); % гармоническая функция

C0=C0+f(i);

end

for k=1:M

C(k)=0;

end

for i=1:N+1

for k=1:M

C(k)=C(k)+f(i)*exp(-j*2*pi*k*(i-1)/N);

end

end

for k=1:M

C(k)=C(k)*(2/N);

end

for i=1:N

y(i)=0;

for k=1:M

y(i)=y(i)+C(k)*exp(j*2*pi*k*(i-1)/N);

end

end

Прямое и обратное комплексное преобразование Фурье с использованием стандартной функции БПФ

i=1:N;

bpfy=fft(f,N);

bpf=(bpfy.*conj(bpfy));%БПФ

bpf=bpf/max(bpf);

f2=ifft(bpfy);%ОБПФ

Возможно разложение и по другим ортонормированным функциям, например, функциям Лагерра, Лежандра, Уолша [9]. О целесообразности этого было написано выше.