Аннулирующий многочлен вектора, пространства

Структура линейного преобразования.

Рассмотрим наименьшее (по включению) инвариантное подпространство, содержащее вектор x. Очевидно, что с вектором x в нем содержится и векторы 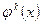, где k=1,2,… . Обозначим через k наибольшее число, при котором система векторов 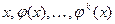линейно независима. Очевидно, что линейная оболочка этих векторов образует наименьшее инвариантное подпространство, содержащее вектор x. Выразим 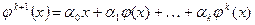. 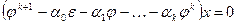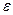Это равенство запишем в виде , где - тождественное преобразование. Слева стоит линейное преобразование, по виду являющееся многочленом от линейного преобразования 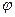. Будем говорить, что многочлен p(t) аннулирует вектор x, если 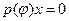. Многочлен наименьшей степени, аннулирующий вектор x, называется минимальным аннулирующим многочленом вектора x.

Минимальный аннулирующий многочлен определен с точностью до числового множителя. Далее, для определенности будем считать коэффициент при старшей степени равным 1.

Свойство 1.1 Аннулирующий многочлен вектора делится без остатка на минимальный аннулирующий многочлен вектора.

Доказательство. Пусть f(t) –аннулирующий многочлен, а p(t) – минимальный аннулирующий многочлен. Разделим f(t) на p(t) с остатком f(t)=p(t)g(t)+r(t). Тогда 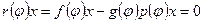. Так как степень r(t) меньше степени p(t), и многочлен r(t) аннулирует вектор x, то единственная возможность r(t)=0.

Теорема 1.1 (Метод и академика Крылова). Пусть векторы 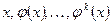линейно независимы и 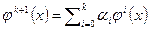, тогда многочлен 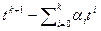является минимальным аннулирующим многочленом вектора x.

Доказательство. Очевидно, что многочлен 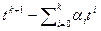является аннулирующим для вектора x. Допустим, он не является минимальным аннулирующим многочленом. Следовательно, найдется аннулирующий многочлен меньшей степени 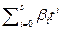, что 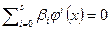. Последнее равенство не возможно в силу линейной независимости системы векторов .

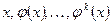Теорема 1.2 Минимальный аннулирующий многочлен вектора является делителем характеристического многочлена.

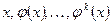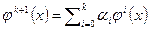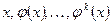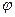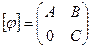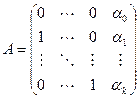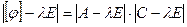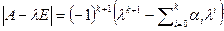Доказательство. Пусть система векторов - линейно независима и . Дополним систему векторов до базиса всего пространства и найдем матрицу линейного преобразования в этом базисе. Эта матрица имеет блочный вид , где - блок порядка k+1. По теореме Лапласа , а - минимальный аннулирующий многочлен вектора x.

Следствие 1.1. (теорема Гамильтона – Кэли) Линейное преобразование является корнем своего характеристического многочлена.

Доказательство. Пусть 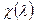- характеристический многочлен. Тогда для любого x имеем 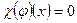, и, следовательно, .

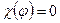Будем говорить, что многочлен p(t) аннулирует подпространство W, если он аннулирует каждый вектор из W. Аннулирующий многочлен подпространства W наименьшей степени называется минимальным аннулирующим многочленом подпространства W. Как и минимальный аннулирующий многочлен вектора, минимальный аннулирующий многочлен подпространства определен с точностью до множителя. Для определенности, будем считать старший коэффициент минимального аннулирующего многочлена подпространства равным 1.

Свойство 1.2. Аннулирующий многочлен подпространства делится без остатка на минимальный аннулирующий многочлен этого же подпространства.

Доказательство. Пусть f(t) –аннулирующий многочлен, а p(t) – минимальный аннулирующий многочлен. Разделим f(t) на p(t) с остатком f(t)=p(t)g(t)+r(t). Тогда для вектора x из W справедливо равенство 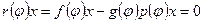. Так как степень r(t) меньше степени p(t), и многочлен r(t) аннулирует любой вектор x из W, то единственная возможность r(t)=0.

Теорема 1.3. Минимальный аннулирующий многочлен подпространства равен наименьшему общему кратному минимальных аннулирующих базисных векторов.

Доказательство. Пусть 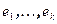- базис подпространства W, h - минимальный аннулирующий многочлен подпространства W,а 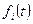- минимальный аннулирующий многочлен вектора 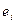, где i=1,…,k. Многочлены 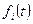являются делителями h(t) (Свойство 1.1). С другой стороны, наименьшее общее кратное этих многочленов аннулирует все базисные векторы, а значит и любой вектор из W.

Следует отметить, что хотя построение минимального аннулирующего многочлена подпространства и зависит от выбора базиса подпространства, однако сам минимальный аннулирующий многочлен не зависит от выбора этого базиса.

Следствие 1.2. Минимальный аннулирующий многочлен подпространства является делителем характеристического многочлена.

Доказательство. Пусть 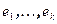- базис подпространства W, а 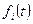- минимальный аннулирующий многочлен вектора 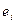, где i=1,…,k. Многочлены 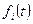являются делителями характеристического многочлена (Теорема 1.2), следовательно, характеристический многочлен делится и на их наименьшее общее кратное, равное минимальному аннулирующему многочлену подпространства.

Если в качестве подпространства взять все пространство, то минимальный аннулирующий многочлен подпространства называется минимальным аннулирующим многочленом.

Следствие 1.3. Минимальный аннулирующий многочлен является делителем характеристического многочлена и имеет то же самое множество корней.

Доказательство очевидным образом вытекает из следствия 1.1 и свойства 1.2.

В заключение приведем полезное свойство.

Свойство 1.3 Пусть 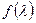- минимальный аннулирующий многочлен вектора 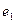, 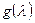- минимальный аннулирующий многочлен вектора 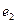, и 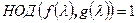. Тогда минимальный аннулирующий многочлен вектора 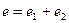равен .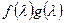

Доказательство. Пусть 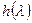- минимальный аннулирующий многочлен вектора e. Из равенств 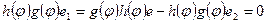вытекает, что 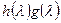- аннулирующий многочлен 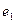и, значит, делится без остатка на 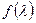(Свойство 1.1). По условиям 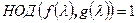и, следовательно, 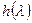делится на 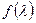без остатка. Аналогичным образом устанавливается делимость 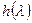на 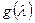. Следовательно, 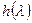делится на произведение 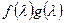. Поскольку 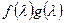является аннулирующим многочленом вектора e, то свойство доказано.

1.2 Расщепление пространства в прямую сумму инвариантных подпространств

Пусть V – линейное пространство размерности n над полем комплексных чисел, 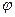- линейное преобразование линейного пространства V, 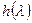- аннулирующий многочлен всего пространства V.

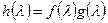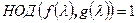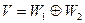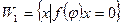Теорема 1.4 Пусть и , тогда линейное пространство V представляется в виде прямой суммы инвариантных подпространств , где и .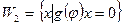

Доказательство. Подпространство 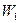является ядром линейного преобразования 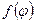и по свойству 7.4 инвариантно относительно 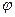. Аналогично доказывается инвариантность подпространства .

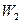Поскольку 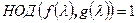, то найдутся многочлены 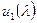и 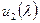, для которых 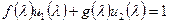. Подставив в данное равенство вместо переменной 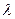линейное преобразование 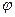, получим 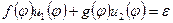. Таким образом, для любого вектора x из V справедливо равенство 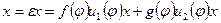. Вектор 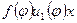принадлежит 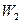, так как 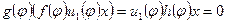. Аналогично, вектор 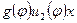принадлежит 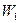. Тем самым показано, что пространство V является суммой подпространств 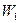и .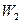

Для доказательства теоремы осталось показать, что пересечение подпространств 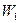и 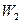состоит из одного нулевого вектора. Действительно, пусть 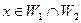. Тогда 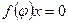и 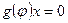, а, значит, .

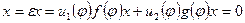Следствие 1.4 Если в условиях теоремы 1.1 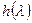- минимальный аннулирующий многочлен пространства, то 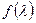- минимальный аннулирующий многочлен 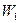, а 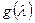- минимальный аннулирующий многочлен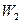

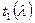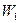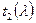Доказательство. Пусть - минимальный аннулирующий многочлен подпространства , а - минимальный аннулирующий многочлен подпространства 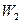. Поскольку V - прямая сумма инвариантных подпространств 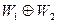, то 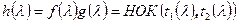. По определению минимального аннулирующего многочлена 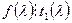и 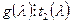, следовательно, 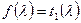и .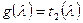

Следствие 1.5. Пусть 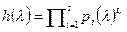- аннулирующий многочлен пространства, разложенный в произведение неприводимых множителей. Тогда линейное пространство представляется в виде прямой суммы инвариантных подпространств 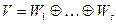, где 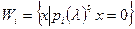. Если 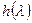- минимальный аннулирующий многочлен, то 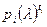- минимальный аннулирующий многочлен .

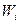Доказательство очевидно.

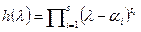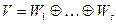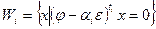Следствие 1.6. Пусть V – линейное пространство над полем комплексных чисел, - минимальный аннулирующий многочлен V. Тогда линейное пространство представляется в виде прямой суммы инвариантных подпространств , где и 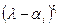- минимальный аннулирующий многочлен .

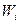Доказательство очевидно.