Определение степени близости функций

Рассмотрим задачу определения взаимоотношения между сигналами f(t) и g(t) по их векторному представлению. Конечно, два значения сигнала весьма слабо характеризуют сигналы, но, как будет показано дальше, выводы, сделанные по двум выборкам могут быть распространены на случай сколь угодно большого количества выборок.

Итак, определим векторы, содержащие по два элемента из выборки каждого сигнала, иначе говоря, двумерные векторы. Обозначим их как f и g:

f=( f₁ , f₂), g=( g₁ , g₂ )

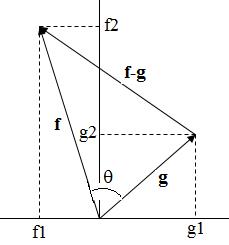
Если сигналы выразить через векторы, то исследование отношений между сигналами будет равносильно исследованию отношений между векторами. Исследование может заключаться в определении степени близости функций. В векторном представлении это соответствует расстоянию между векторами. Обозначим d(f,g) расстояние между векторами f и g.Чемменьше значение d, тем ближе векторы f и g, а, значит, и сильнее между ними взаимосвязь.

Рис. 5.1.

Величину вектора f (абсолютное значение) обозначим как ||f ||.Используя компоненты вектора f,получим:

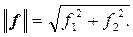
||f ||называют также нормой вектораf.

Итак, из рис. 1 видно, что расстояние между векторами f и gесть норма вектораf – g.Это можно записать, используя компоненты векторов, в следующем виде:

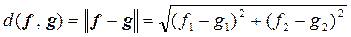
Однако, норма вектора характеризует лишь величину вектора разности, но не учитывает его направления.

Для выражения связи между векторами используют скалярное произведение. Скалярное произведение между f и g обозначается как 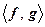и определяется как

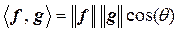
Следовательно

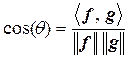
Обозначим эту величину

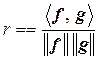
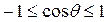, следовательно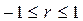

Величина r выражает силу связи между векторами f и g через угол между ними. Если направления f и g совпадают, т.е. если 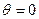, то r принимает максимальное значение, равное 1. С увеличением угла 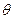значение r уменьшается. Если r=0, т.е. 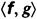=0, то векторы f и gвзаимно перпендикулярны. Назовем величину r коэффициентом корреляции.

Как видно из приведенного выше соотношения, r зависит от угла между векторами и не зависит от нормы векторов. Выразим скалярное произведение, используя компоненты вектора:

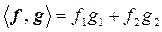
Чтобы вывести эту формулу, применим теорему косинусов для векторов:

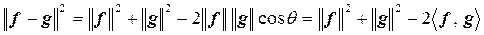
Следовательно

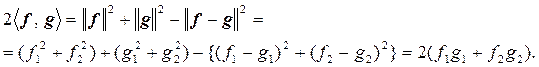
Подставим полученные результаты в выражение коэффициента корреляции и представим r следующим образом:

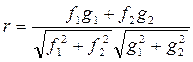
Представляя это выражение через составляющие вектора, получим

Из этого соотношения можно вывести выражение для коэффициента корреляции в N-мерном пространстве:

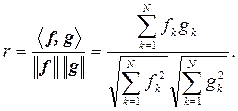
Обобщив последнее соотношение можно вывести формулу для скалярного произведения функций. Используя соответствие вектор 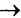функция, сумма 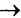интеграл, определим скалярное произведение функций f(t) и g(t) на интервале [a,b] :

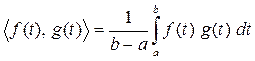
Скалярное произведение функции f(t) на саму себя:

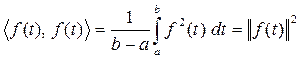
Это означает, что f(t) имеет те же свойства, какими обладает многомерный вектор в векторном пространстве. То, что мы смогли определить скалярное произведение функций, означает также и то, что мы приняли и учли такое понятие, как угол между функциями. Если функции f(t) и g(t) в пространстве функций расположены под углом q, то коэффициент корреляции можно определить так же, как и в случае векторов, используя норму и скалярное произведение:

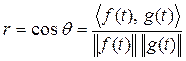
Если записать подробно, то получим:

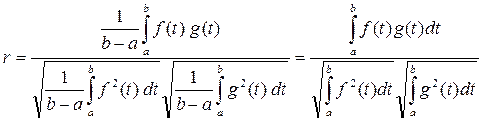
Как и прежде, коэффициент корреляции показывает степень «похожести» функций. Причем r принимает значения от -1 до 1. Чем больше значение r по абсолютной величине, тем они более похожи.