Геометрическое приложение определенного интеграла
1. Вычисление площади плоской фигуры (области (D))
а) Линии, ограничивающие область (D), заданы в декартовых координатах
Случай 1. Площадь области (D), ограниченной прямыми 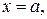
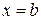 (b>a) и непрерывными кривыми
(b>a) и непрерывными кривыми 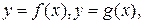 где
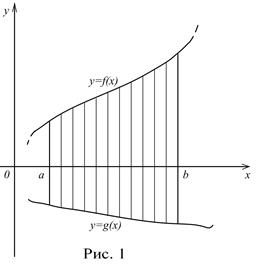
где 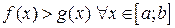 (рис. 1), находится по формуле:
(рис. 1), находится по формуле:
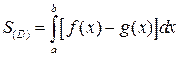 (1)
(1)
Случай 2. Площадь области (D), ограниченная прямыми y=c, y=d (d>c) и
непрерывными кривыми 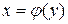 и
и 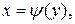 где
где 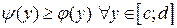 (рис. 2), находится по формуле:
(рис. 2), находится по формуле:
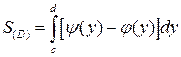 (2)
(2)
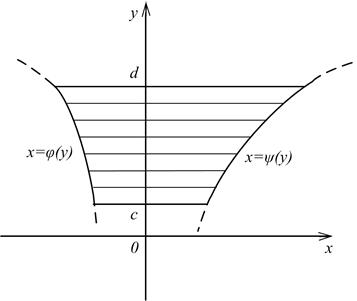
Рис. 2
б) Линии, ограничивающие область (D), заданы в параметрической форме.
Формула для вычитания площади области (D), ограниченной прямыми x=a, x=b (b>a), непрерывной линией, заданной параметрически уравнениями:
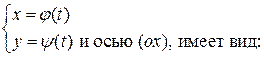
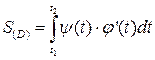 , где
, где 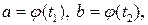 ψ(t)≥0∀t∈[t1;t2] (3)
ψ(t)≥0∀t∈[t1;t2] (3)
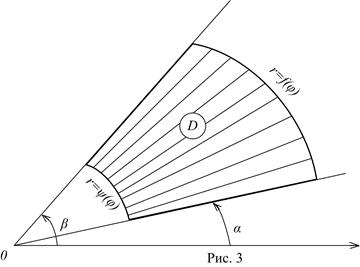
в) Линии, ограничивающие область (D), заданы в полярной системе координат
Площадь области (D), ограниченной полярными лучами φ=α, φ=β (β>α) и непрерывными полярными кривыми: r=f(φ), r=ψ(φ), где 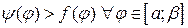 находится по формуле:
находится по формуле:
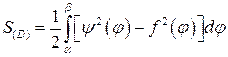 (4)
(4)
2. Вычисление объема тела вращения
Формула для вычисления объема тела вращения, образованного вращением криволинейной трапеции вокруг оси (ox), имеет вид:
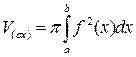 (5)
(5)
(рис. 4)
а вокруг оси (oy):
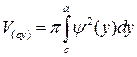 (6)
(6)
(рис. 5)


Дата добавления: 2017-01-08; просмотров: 1635;











