Интегрирование посредством разложения подынтегральной функции на слагаемые
Метод интегрирования разложением функции на слагаемые базируется на линейных свойствах неопределенного интеграла (4 и 5). Если подынтегральная функция представляет алгебраическую сумму нескольких слагаемых, то согласно свойству (5) можно интегрировать каждое слагаемое отдельно. Это позволяет многие интегралы свести к сумме более простых интегралов.
Примеры с решениями
Пример 1. Найти интеграл 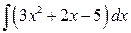
Решение.
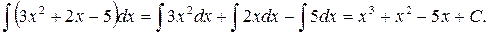
Ответ: 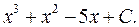
Пример 2. Найти интеграл 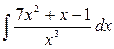
Решение. Разлагаем подынтегральную функцию на слагаемые, деля числитель почленно на знаменатель.
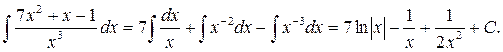
Ответ: 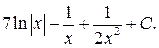
Пример 3. Найти интеграл 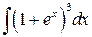
Решение. Возводим в куб и интегрируем каждое слагаемое.
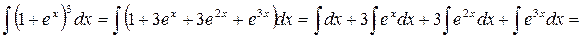
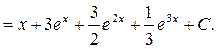
Ответ: 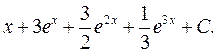
Пример 4. Найти интеграл 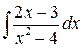
Решение. Разлагаем подынтегральную дробь на две слагаемых дроби, деля числитель почленно на знаменатель.
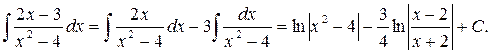
Ответ: 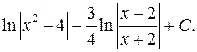
Пример 5.Найти интеграл 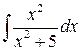
Решение. Выделим в неправильной дроби целую часть и правильную дробь.
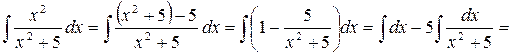
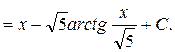
Ответ: 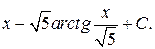
Примеры для самостоятельного решения
1. 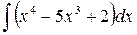
2. 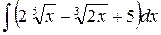
3. 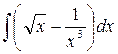
4. 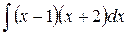
5. 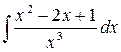
6. 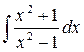
7. 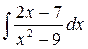
8. 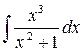
9. 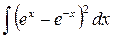
10. 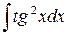
11. 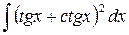
12. 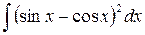
13. 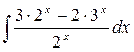
14. 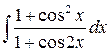
15. 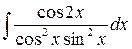
16. 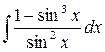
17. 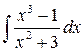
18. 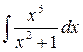
19. 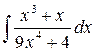
20. 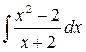
Ответы
1. 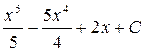 ; 2.
; 2. 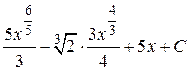 ; 3.
; 3. 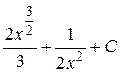 ;
;
4. 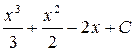 ; 5.
; 5. 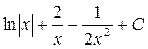 ; 6.
; 6. 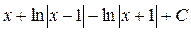 ;
;
7. 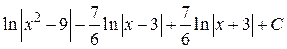 ; 8.
; 8. 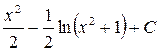 ; 9.
; 9. 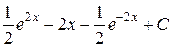 ; 10.
; 10. 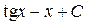 ; 11.
; 11. 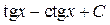 ; 12.
; 12. 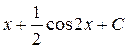 ; 13.
; 13. 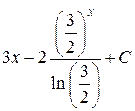 ; 14.
; 14. 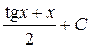 ; 15.
; 15. 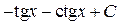 ; 16.
; 16. 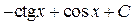 ; 17.
; 17. 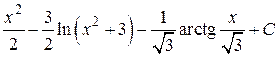 ; 18.
; 18. 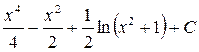 ; 19.
; 19. 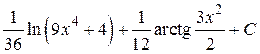 ; 20.
; 20. 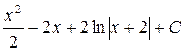 .
.
Дата добавления: 2017-01-08; просмотров: 2863;











