Примеры с решениями. Вычислить площадь, ограниченную линиями
Пример 1. Вычислить площадь, ограниченную линиями: параболой 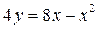 и прямой
и прямой 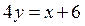 .
.
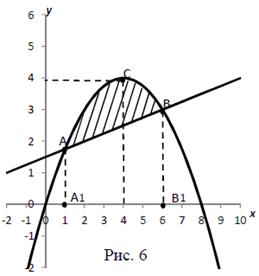
Решение. Построив данные линии, видно, что искомая площадь области ACB (рис.6) ограниченной сверху параболой и снизу прямой, которые пересекаются в точках А (1;  ) и В (6;3), равна разности площадей А1АСВВ1 и А1АВВ1. Тогда площадь области выражается интегралом в соответствии с формулой (1).
) и В (6;3), равна разности площадей А1АСВВ1 и А1АВВ1. Тогда площадь области выражается интегралом в соответствии с формулой (1).
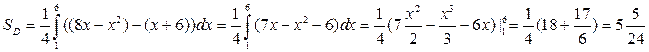
Ответ: 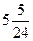 кв. ед.
кв. ед.
Пример 2. Найти площадь, ограниченную эллипсом 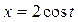 ,
, 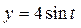 .
.
Решение. Оси координат совпадают с осями симметрии данного эллипса (рис. 7).Четвертую часть искомой площади S, расположенную в первой четверти координатной плоскости, найдем как площадь криволинейной трапеции, прилегающей к Ox:
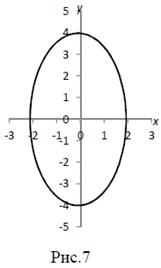
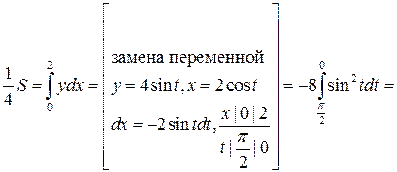
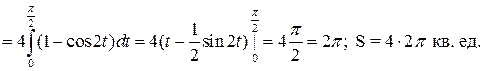
Ответ: S = 8π кв. ед.
Пример 3. Вычислить площадь, ограниченную кардиоидой 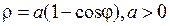 .
.
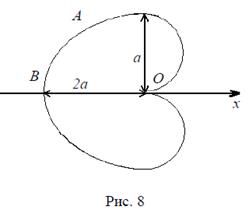
Решение. Кардиоида симметрична относительно полярной оси (рис. 8). Тогда искомая площадь равна удвоенной площади криволинейного сектора OAB. Дуга OAB описывается концом полярного радиуса ρ при изменении угла φ от 0 до π. Используя формулу (4) найдем S.
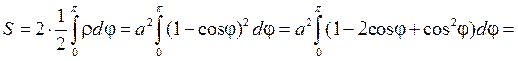
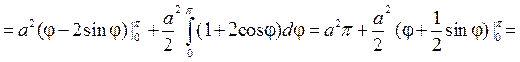
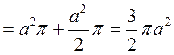
Ответ: 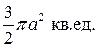
Пример 4. Вычислить объём тела, образовавшегося вращением фигуры, ограниченной линиями 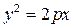 ,
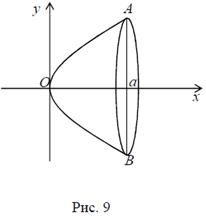
, 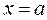 вокруг оси OX (рис. 9).
вокруг оси OX (рис. 9).
Решение. Построив параболу 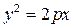 и прямую
и прямую 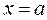 , получим внутреннюю область OAB при вращении её вокруг оси OX, образуется сегмент параболоида вращения. Объем этого тела находим по формуле (5).
, получим внутреннюю область OAB при вращении её вокруг оси OX, образуется сегмент параболоида вращения. Объем этого тела находим по формуле (5).
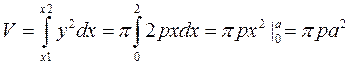
Ответ: 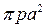 ед. куб.
ед. куб.
Пример 5. Определить работу, произведённую при адиабатическом расширении воздуха, имеющего начальный объём V0 = 1 м3 и давление P0 = 9,8·104 Падо объёма V1 = 10 м3.
Решение. Объём газа в закрытом сосуде и производимое им давление P связаны формулой:
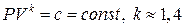
Пусть x (м) – расстояние пройденное поршнем (рис. 6). Предположим, что при изменении x на малую величину Δx испытываемое поршнем давление остаётся неизменным; при этом объём V изменится на ΔV. Работа силы давления на отрезке Δx выразится приближённым равенством: 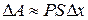 , где S – площадь поршня. Так как
, где S – площадь поршня. Так как 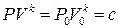 , то
, то 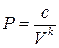 , при этом
, при этом 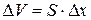 . Следовательно:
. Следовательно:
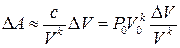 . (Схема II)
. (Схема II)
Интегрируя в пределах от V0 до V1 дифференциальное равенство 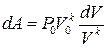 , получим
, получим
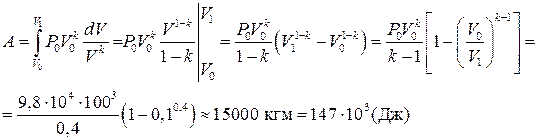
Дата добавления: 2017-01-08; просмотров: 1330;











