Вычисление криволинейного интеграла первого рода
Если кривая L задана уравнением y = j(x), а дуга 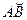 соответствует изменению x Î [a, b], то разбиение
соответствует изменению x Î [a, b], то разбиение 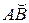 на дуги
на дуги 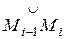 соответствует разбиению [a, b] на части точками a < x1 < x2 < ... < xn = b.
соответствует разбиению [a, b] на части точками a < x1 < x2 < ... < xn = b.
Тогда 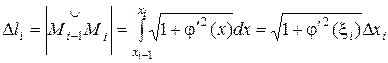 , xiÎ[xi-1, xi]
, xiÎ[xi-1, xi]
(по теореме о среднем).
Тогда 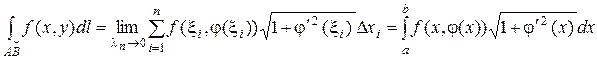
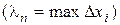
Аналогично, если 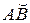 определена уравнением x = y(y), y Î[c, d],то
определена уравнением x = y(y), y Î[c, d],то
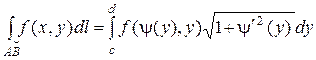 .
.
Если же дугу 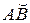 определяют параметрические уравнения
определяют параметрические уравнения 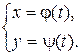 tÎ[a,b], то
tÎ[a,b], то
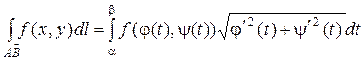 .
.
Таким образом, криволинейный интеграл I рода тоже сводится к ОИ.
Криволинейный интеграл I рода называют еще криволинейным интегралом по длине дуги.
С физической точки зрения 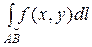 определяет массу неоднородного криволинейного стержня с плотностью r = f(x, y); то есть
определяет массу неоднородного криволинейного стержня с плотностью r = f(x, y); то есть 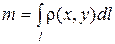 .
.
Свойства криволинейного интеграла первого рода:
1. 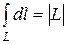 (геометрическая интерпретация криволинейного интеграла I рода)
(геометрическая интерпретация криволинейного интеграла I рода)
2. 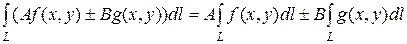 - свойство линейности
- свойство линейности
3. Если 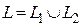 , то
, то 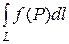 =
= 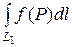 +
+ 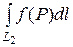 (свойство аддитивности)
(свойство аддитивности)
4. Если f(P) £ g(P), " то 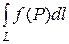 £
£ 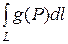
5. Если m £ f(P) £ M, PÎL, то m×|L| £ 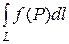 £ M×|L|
£ M×|L|
6. Существует точка QÎ L: 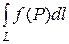 = f(Q)×|L| (Теорема о среднем.)
= f(Q)×|L| (Теорема о среднем.)
Рассмотрим пример вычисления криволинейных интегралов I рода.
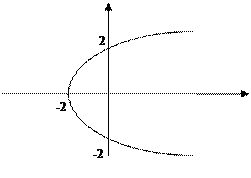 Пример 1.
Пример 1.
Найти массу дуги параболы y2 = 2x + 4 между точками пересечения с осями координат, если плотность масс в любой точке пропорциональна ординате точки дуги.
Решение:
r (x, y) = ky, y ³ 0, x = 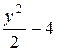 , y Î [0, 2]. Тогда
, y Î [0, 2]. Тогда
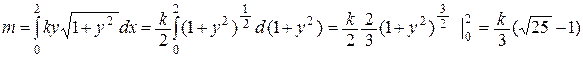 (ед. массы)
(ед. массы)
3. Криволинейный интеграл II рода
Рассмотрим пространство R2. Пусть в области DÌR2 определены две непрерывные функции P(x,y), Q(x,y), тогда в любой точке М(x,y) Î D определена векторная функция `F(x, y) = (P(x, y); Q(x, y)), которую в векторной форме можно записать в виде: 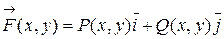 .
.
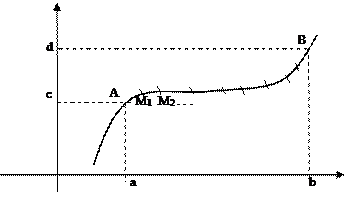
Пусть функции P(x, y) и Q(x, y) определены в точках гладкой дуги 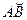 кривой L Ì D. Разобьем дугу
кривой L Ì D. Разобьем дугу 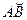 на части точками М1,М2, ...Мn. На каждой дуге
на части точками М1,М2, ...Мn. На каждой дуге 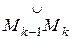 возьмем произвольную точку
возьмем произвольную точку 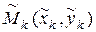 и вычислим значение
и вычислим значение 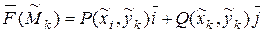 .
.
Пусть [a, b]и[c, d] – проекции 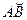 на OX и OY соответственно, т.е. xÎ[a,b], y Î [c, d], когда М(х, у) Î
на OX и OY соответственно, т.е. xÎ[a,b], y Î [c, d], когда М(х, у) Î 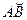 . Каждую частичную дугу спроектируем на оси координат, получим разбиение отрезков [a, b]и[c, d] на n частей, длины частичных интервалов обозначим соответственно Dхk и Dyk. Составим интегральную сумму вида:
. Каждую частичную дугу спроектируем на оси координат, получим разбиение отрезков [a, b]и[c, d] на n частей, длины частичных интервалов обозначим соответственно Dхk и Dyk. Составим интегральную сумму вида:
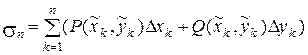 .
.
Эта сумма представляет собой сумму скалярных произведений векторов 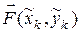 на векторы
на векторы 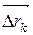 , где
, где 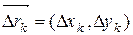 , т.е.
, т.е. 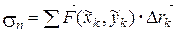
Обозначим 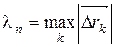
Определение 5.1
Если существует 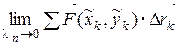 , не зависящий ни от способа разбиения дуги
, не зависящий ни от способа разбиения дуги 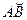 на части, ни от выбора точки
на части, ни от выбора точки 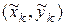 , то этот предел называется криволинейным интегралом II рода и обозначается
, то этот предел называется криволинейным интегралом II рода и обозначается 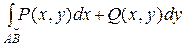 или
или 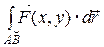 .
.
Итак, криволинейный интеграл II рода
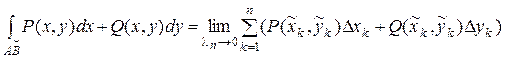 ,
,
Заметим, что условие 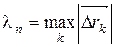 →0 равносильно условиям
→0 равносильно условиям 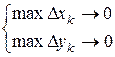
В отличие от криволинейного интеграла I рода, который еще называют интегралом по длине дуги, криволинейный интеграл II рода называют криволинейным интегралом по координатам.
Свойства:
1. 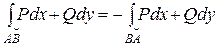 - меняет знак при изменении ориентации кривой (направления движения по кривой).
- меняет знак при изменении ориентации кривой (направления движения по кривой).
2. Свойство линейности, аддитивности (АВ = АС + СВ) аналогичны свойствам криволинейного интеграла I рода. В частности, 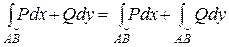
3. Связь между криволинейными интегралами I и II рода выражает формула: 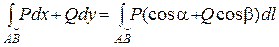 ,
,
где (cosa,cosb) – направляющие косинусы касательной к дуге АВ в любой ее точке.
Способы вычисления криволинейного интеграла II рода:
1) Если АВ: y = j(x), x Î [a, b], то dy = j¢(x)dx и
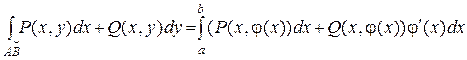
2) Если АВ: x = y(y), y Î [c, d],то dx = y¢(y)dy и
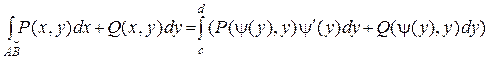
3) Если АВ: 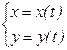 , t Î [a,b], dx = x¢(t)dt, dy = y¢(t)dt, то
, t Î [a,b], dx = x¢(t)dt, dy = y¢(t)dt, то
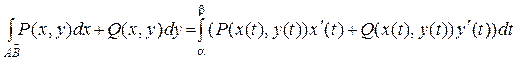
Аналогично можно дать определение криволинейного интеграла II рода по пространственной кривой
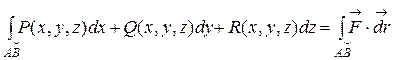
Пример 2.
Вычислить 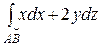 , где АВ – отрезок прямой между точками В(1, 1, 1), А(0, 0, 2).
, где АВ – отрезок прямой между точками В(1, 1, 1), А(0, 0, 2).
Решение:Найдем уравнение АВ:
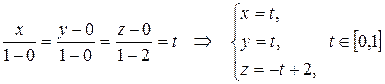 .
.
Тогда 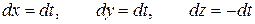 , значит,
, значит,
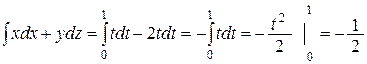 .
.
Физический смысл криволинейного интеграла II рода:
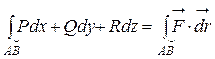

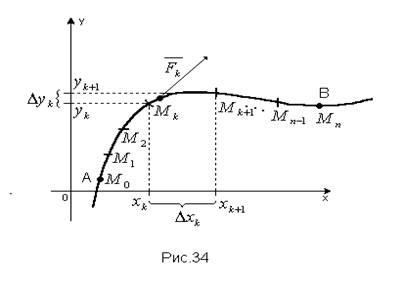 определяет работу силы
определяет работу силы 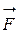 при перемещении материальной точки вдоль кривой L из положения А в положение В. Действительно,
при перемещении материальной точки вдоль кривой L из положения А в положение В. Действительно,  пусть материальная точка M(x,y) движется вдоль некоторой плоской (можно аналогично рассмотреть и пространственную) кривой L от точки A к точке B. Пусть вдоль кривой действует сила
пусть материальная точка M(x,y) движется вдоль некоторой плоской (можно аналогично рассмотреть и пространственную) кривой L от точки A к точке B. Пусть вдоль кривой действует сила 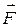 , которая меняется по величине и направлению при перемещении точки M, т.е. сила
, которая меняется по величине и направлению при перемещении точки M, т.е. сила 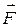 является функцией точки:
является функцией точки: 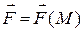 . Найдём работу A силы при перемещении точки из положения A в положение B.
. Найдём работу A силы при перемещении точки из положения A в положение B.
Как известно, в случае, когда сила постоянна, а путь прямолинейный, работа равна 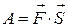 (*), т.е. скалярному произведению вектора силы
(*), т.е. скалярному произведению вектора силы 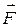 на вектор перемещения
на вектор перемещения 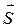 . Воспользуемся этим фактом и для решения поставленной задачи.
. Воспользуемся этим фактом и для решения поставленной задачи.
 1) Разобьём дугу AB в направлении от точки A к точке B на n частей точками A=M0,M1, M2,…, Mn=B и обозначим через
1) Разобьём дугу AB в направлении от точки A к точке B на n частей точками A=M0,M1, M2,…, Mn=B и обозначим через 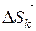 вектор
вектор 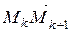 .
.  Тогда
Тогда
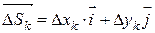
(рис.34). Пусть λ – наибольшая из длин этих векторов, т.е.
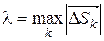 .
.



 2) На каждой элементарной дуге выберем произвольную точку
2) На каждой элементарной дуге выберем произвольную точку 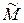 k(xk,yk) и предположим, что в пределах каждой элементарной дуги сила
k(xk,yk) и предположим, что в пределах каждой элементарной дуги сила 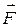 постоянна и равна
постоянна и равна 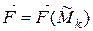 . Тогда в силу (*), скалярное произведение
. Тогда в силу (*), скалярное произведение 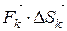 можно рассматривать как приближённое значение работы Ak силы вдоль дуги
можно рассматривать как приближённое значение работы Ak силы вдоль дуги 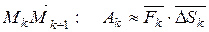 .
.
Пусть 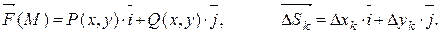
Тогда 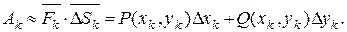

3) Искомая работа A силы на всей дуге AB будет приближённо равна

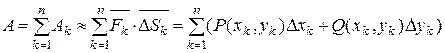
 и это приближённое равенство тем точнее, чем меньше λ.
и это приближённое равенство тем точнее, чем меньше λ.
 4) Следовательно, истинное значение работы A силы
4) Следовательно, истинное значение работы A силы 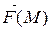 при перемещении точки M по дуге AB получим, переходя к пределу при λ→0:
при перемещении точки M по дуге AB получим, переходя к пределу при λ→0: 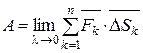 =
= 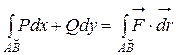 .
.
Рассмотрим замкнутую кривую C, будем называть ее замкнутымконтуром. Ориентацию на этой кривой выберем следующим образом: если при движении точки М вдоль кривой ограниченная этим контуром область G остается слева, то направление движения (ориентацию на кривой) будем считать положительным. В противном случае – отрицательным.
 | |||
 | |||
Криволинейный интеграл II рода по замкнутому контуру будем обозначать 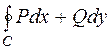
Справедлива
Дата добавления: 2017-11-21; просмотров: 2032;











