Вычисление двойного интеграла в декартовой системе координат.
Предположим, что D – плоская область, лежащая в некоторой плоскости и введем в этой плоскости декартову систему координат.
Область D назовем правильной, если любая прямая, параллельная декартовым осям, пересекает ее не более чем в двух точках.
Можно показать, что замкнутую ограниченную область с кусочно-гладкой границей можно представить в виде объединения правильных областей, не имеющих общих внутренних точек. Поэтому интеграл по области D можно вычислять как сумму интегралов (свойство 2) по правильным областям. Будем считать, что нам надо вычислить двойной интеграл по правильной области.
| Вспомним формулу для вычисления объема тела по площадям параллельных сечений
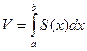 , где , где 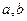 - «крайние» точки области D по x., - «крайние» точки области D по x., 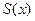 - площадь сечения тела одной из параллельных плоскостей (при фиксированном x). Эта плоскость пересекается с плоскостью OXY по прямой, параллельной оси OY, соединяющей точку входа в область j(x) с точкой выхода f(x). Графики функций j(x), f(x) образуют границу области D. - площадь сечения тела одной из параллельных плоскостей (при фиксированном x). Эта плоскость пересекается с плоскостью OXY по прямой, параллельной оси OY, соединяющей точку входа в область j(x) с точкой выхода f(x). Графики функций j(x), f(x) образуют границу области D. 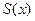 = = 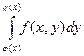 - площадь криволинейной трапеции.. - площадь криволинейной трапеции..
|
Подставляя 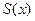 в формулу для объема, получим
в формулу для объема, получим 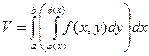 . Это повторный интеграл, вернее один из них. Второй повторный интеграл можно получить, вводя сечения, параллельные оси OX. По аналогии
. Это повторный интеграл, вернее один из них. Второй повторный интеграл можно получить, вводя сечения, параллельные оси OX. По аналогии 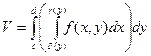 . По смыслу двойного интеграла (объем цилиндрического тела)
. По смыслу двойного интеграла (объем цилиндрического тела)
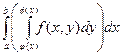 =
= 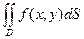 =
= 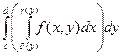
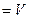
Примеры. Записать двойной интеграл по заданной области и повторные интегралы.
1.
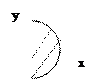  
  1. 1.  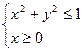
| 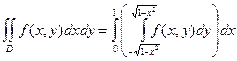 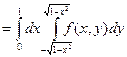 = = 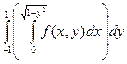 = = 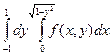
|
   2. 2. 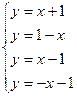
| 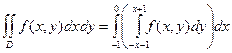 + + 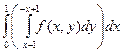 = = 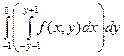 + + 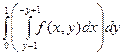
|
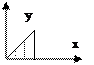 3. 3. 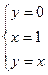
| 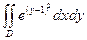 = = 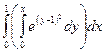 ( внутренний интеграл не берется)= ( внутренний интеграл не берется)=
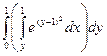 = = 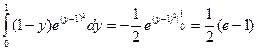
|
Дата добавления: 2017-11-21; просмотров: 1633;











