Вычисление площади поверхности с помощью двойного интеграла.
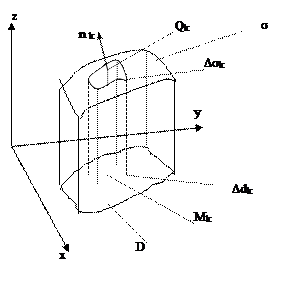 
| Пусть поверхность s, площадь которой надо вычислить, задана уравнением F(x, y, z) = 0 или уравнением z = f(x, y). Введем разбиение s на ячейки Dsk, не имеющие общих внутренних точек, площадью Dvk. Пусть область s и ячейки Dsk проектируются на плоскость OXY в область D и ячейки Ddk площадью Dsk. Отметим на ячейке Ddk точку Mk. В точке Qk (ячейки Dsk), которая проектируется в точку Mk, проведем единичный вектор нормали nk {cosak, cosbk, cosgk} к поверхности s и касательную плоскость. Если приближенно считать равными площадь Dvk ячейки Dsk и площадь ее проекции на касательную плоскость, |
то можно считать справедливым соотношение Dvk cosgk = Dsk. Выразим отсюда
Dvk=Dsk/ cosgk. Будем измельчать разбиение при условии max diam Dsk ®0, что для кусочно-гладкой поверхности, не ортогональной плоскости OXY, равносильно max diam Ddk ®0. Вычислим площадь поверхности как двойной интеграл
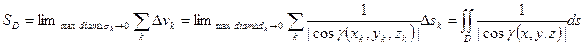 .
.
Сюда остается лишь подставить 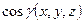 .
.
Если поверхность s задана уравнением F(x, y, z) = 0, то 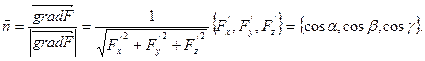
Поэтому в этом случае 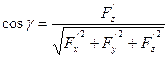 ,
, 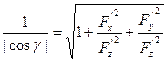 .
.
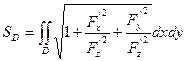 .
.
Если поверхность задана уравнением z = f(x, y), то уравнение это можно
свести к уравнению F(x, y, z) = 0 и применить выведенную формулу:
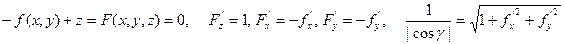
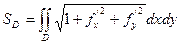 .
.
Пример. Вычислить площадь поверхности конуса 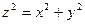 , ограниченной плоскостями
, ограниченной плоскостями 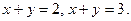
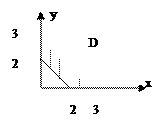  
| 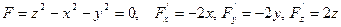
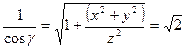 . .
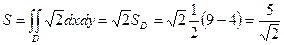 . .
|
Дата добавления: 2017-11-21; просмотров: 1506;











