Вычисление поверхностного интеграла II рода
Пусть гладкая поверхность S задана уравнением z = z (x,y) . Определена в замкнутой области G – проекции S на плоскость ОХУ . Рассмотрим на поверхности S
R(x,y,z) – непрерывная функция .
Разобьём S произвольно на n частей G1 , G2 , . . . ,Gn .
Выберем по произвольной точке Мi (xi , hi, Vi) .
Составим интегральную сумму :
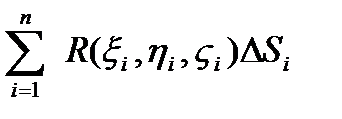 =
= 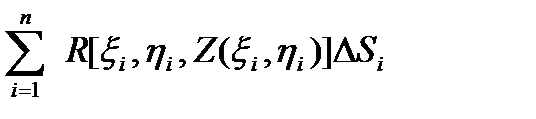 ,
,
где DSi – площадь Gi , так как точка Vi = Z(xi , hi) .
Переходя в (4.1) к пределу при d®0 получаем
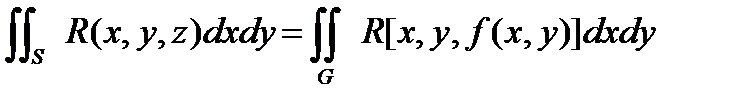 .
.
Аналогично :
. 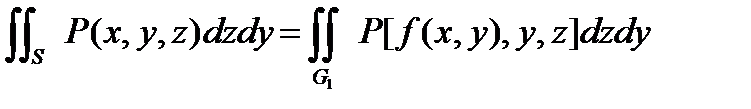
G1 – проекция S на Oyz .
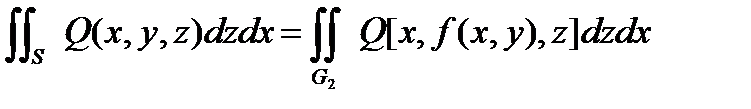
G2 – проекция S на Ozх .
Связь между поверхностными интегралами I и II рода
Пусть гладкая ориентированая поверхность , на которой задана непрерывная вектор – функция 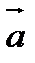 (М) = [ P(x,y,z), Q(x,y,z) , R(x,y,z)] ,
(М) = [ P(x,y,z), Q(x,y,z) , R(x,y,z)] , 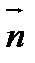 (M) – единичная нормаль = ( cosa , cosb , cosg ) , тогда
(M) – единичная нормаль = ( cosa , cosb , cosg ) , тогда
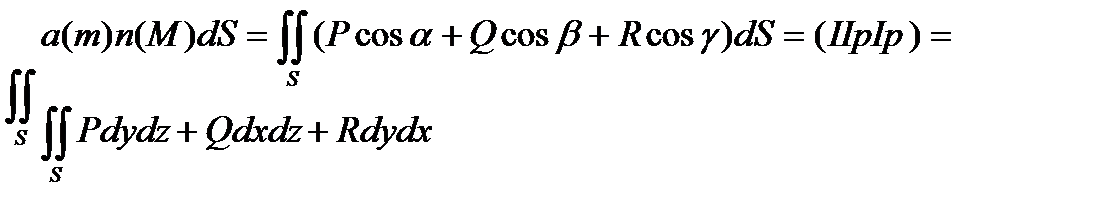
Отсюда видно , что если выбрать другую сторону поверхности , то направляющий косинус изменит знак .
Пример 6.8.11.Вычислить
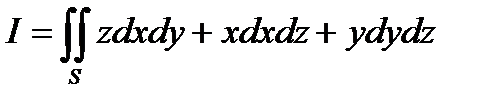 , где S - поверхность треугольника , образованного пересечением плоскости х – у +z = 1 с координатными плоскостями : х = 0 , у = 0 , z = 0
, где S - поверхность треугольника , образованного пересечением плоскости х – у +z = 1 с координатными плоскостями : х = 0 , у = 0 , z = 0  в верхней стороне поверхности .
в верхней стороне поверхности .
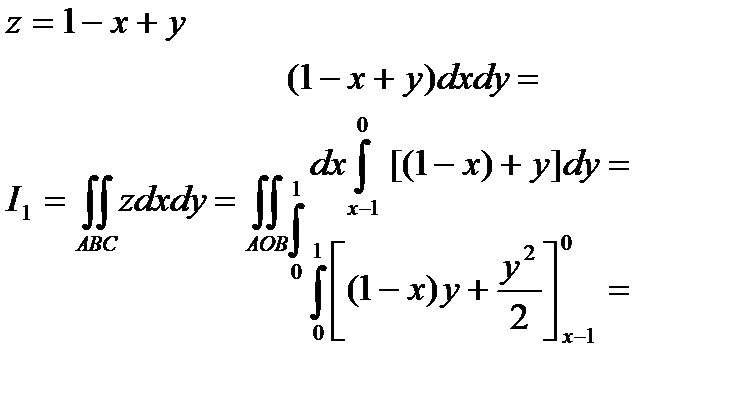
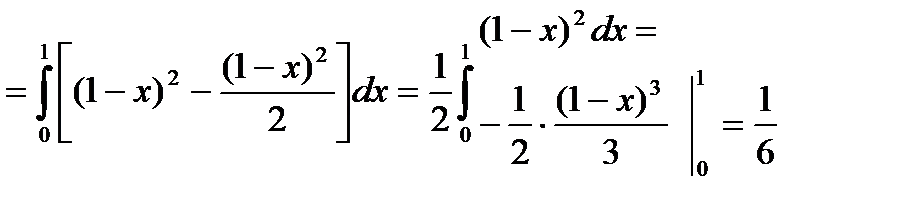
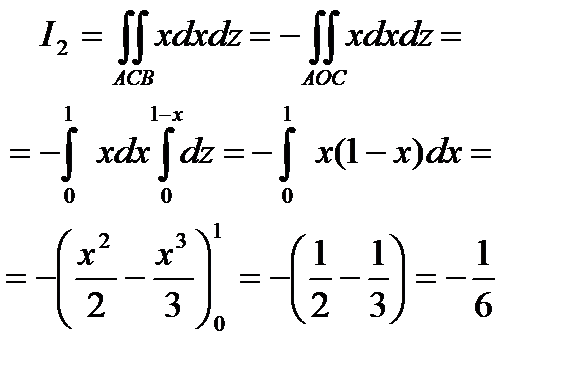
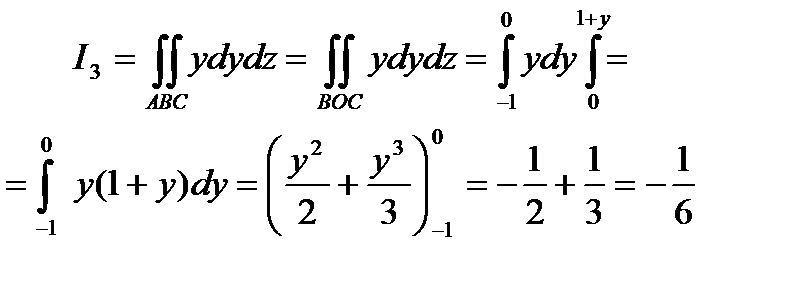
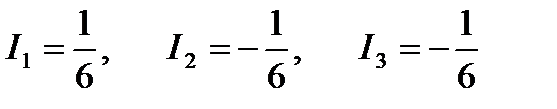
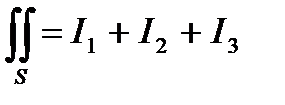 .
.
Формула Остроградского
Дата добавления: 2016-06-05; просмотров: 2427;











