Приложения определенного интеграла
Понятие определенного интеграла вследствие его абстрактности широко применяется при вычислении различных геометрических и физических величин.
Для вычисления некоторой величины с помощью определенного интеграла можно использовать следующие общие схемы решения.
Схема I
1. Разбиваем величину 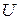 на
на 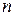 слагаемых
слагаемых 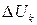 :
:
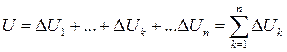
2. Выражаем приближенно каждое слагаемое 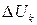 в виде произведения:
в виде произведения:
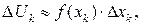
где 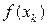 – данная или определяемая из условий задачи функция,
– данная или определяемая из условий задачи функция, 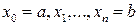 – точка интервала
– точка интервала 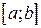 , разбивающие его на
, разбивающие его на 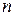 равных частей с длинами
равных частей с длинами 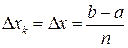 .
.
3. Представляем приближенно значение 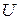 в виде интегральной суммы:
в виде интегральной суммы:
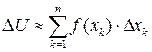
4. Если из условия задачи следует, что погрешность этого приближенного равенства стремится к 0 при 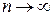 , то искомая величина
, то искомая величина 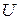 выражается определенным интегралом:
выражается определенным интегралом:
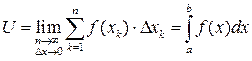
Схема II
1. Пусть величина 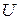 получает приращение
получает приращение 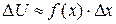 , соответствующее изменению
, соответствующее изменению 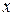 на малую величину
на малую величину 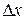 , причем
, причем 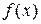 рассматривается как данная или определяемая из условий задачи функция от
рассматривается как данная или определяемая из условий задачи функция от 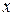 .
.
2. Заменив приращение 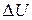 дифференциалом
дифференциалом 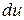 (главная линейная часть приращения дифференцируемой функции) и
(главная линейная часть приращения дифференцируемой функции) и 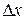 – дифференциалом
– дифференциалом 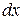 (
( 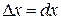 ), получим
), получим
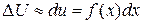
3. Интегрируя это равенство в пределах от 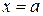 до
до 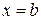 , получим
, получим
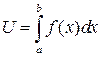
Дата добавления: 2017-01-08; просмотров: 1420;











