Непосредственное интегрирование
а) Работа с таблицей: если предложенный интеграл оказался одним из табличных интегралов, то в этом случае требуется безошибочно найти соответствующую формулу таблицы основных интегралов и воспользоваться ею.
б) Подведение под знак дифференциала: предложенный интеграл удается свести к табличному с помощью изменения переменой интегрирования или за счёт преобразований под знаком дифференциала. Это основано на определении дифференциала d(j(x)) = j '(x)dx. Часто используют следующие формулы:
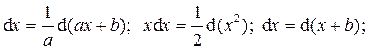
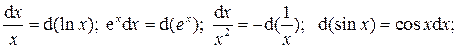
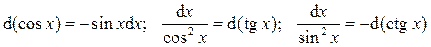
и т.д.
Если известен результат интегрирования 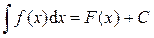 , то равенство
, то равенство 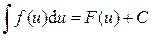 будет справедливо для любой дифференцируемой функции u = j(x).
будет справедливо для любой дифференцируемой функции u = j(x).
Примеры с решениями
Пример 1.
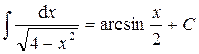 (таблица – формула 14)
(таблица – формула 14)
Пример 2.
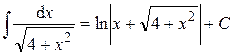 (таблица – формула 16)
(таблица – формула 16)
Пример 3.
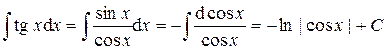 (формула: –
(формула: – 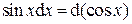 ).
).
Ответ: 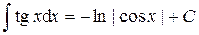 .
.
Пример 4.
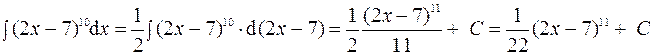
(формула: – 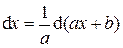 ).
).
Ответ: 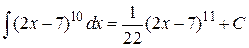 .
.
Пример 5.
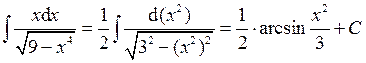 (формула: –
(формула: – 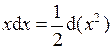 ).
).
Ответ: 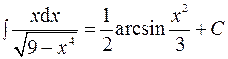 .
.
Пример 6.
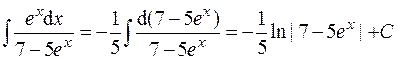 ( формула: –
( формула: – 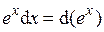 ).
).
Ответ: 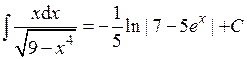 .
.
Пример 7.
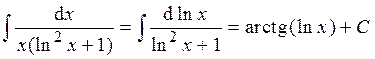 (формула: –
(формула: – 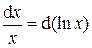 ).
).
Ответ: 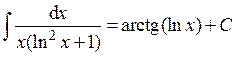 .
.
Примеры для самостоятельного решения
1. 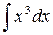
2. 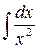
3. 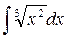
4. 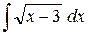
5. 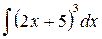
6. 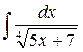
7. 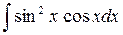
8. 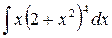
9. 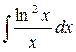
10. 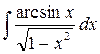
11. 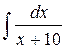
12. 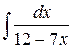
13. 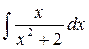
14. 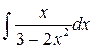
15. 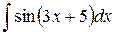
16. 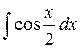
17. 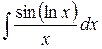
18. 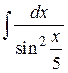
19. 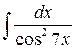
20. 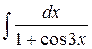
21. 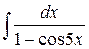
22. 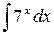
23. 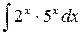
24. 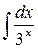
25. 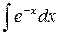
26. 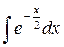
27. 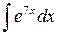
28. 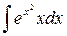
29. 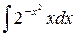
30. 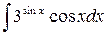
31. 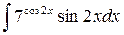
32. 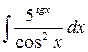
33. 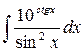
34. 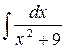
35. 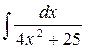
36. 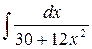
37. 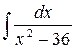
38. 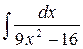
39. 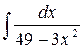
40. 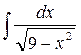
41. 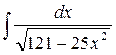
42. 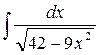
43. 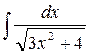
44. 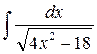
45. 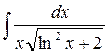
46. 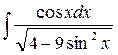
47. 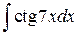
48. 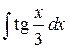
49. 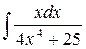
50. 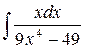
Ответы
1. 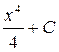 ; 2.
; 2. 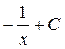 ; 3.
; 3. 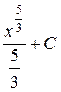 ; 4.
; 4. 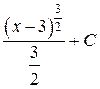 ; 5.
; 5. 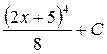 ; 6.
; 6. 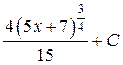 ; 7.
; 7. 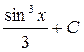 ; 8.
; 8. 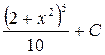 ; 9.
; 9. 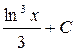 ;10.
;10. 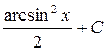 ; 11.
; 11. 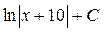 ;12.
;12. 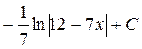 ;13.
;13. 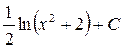 ; 14.
; 14. 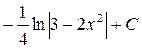 ; 15.
; 15. 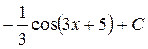 ; 16.
; 16. 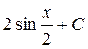 ; 17.
; 17. 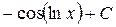 ; 18.
; 18. 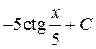 ; 19.
; 19. 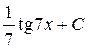 ; 20.
; 20. 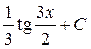 ; 21.
; 21. 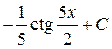 ; 22.
; 22. 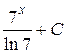 ; 23.
; 23. 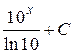 ; 24.
; 24. 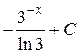 ; 25.
; 25. 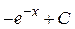 ; 26.
; 26. 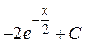 ; 27.
; 27. 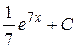 ; 28.
; 28. 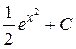 ; 29.
; 29. 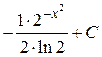 ; 30.
; 30. 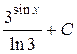 ; 31.
; 31. 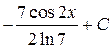 ; 32.
; 32. 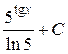 ; 33.
; 33. 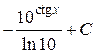 ; 34.
; 34. 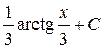 ; 35.
; 35. 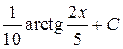 ; 36.
; 36. 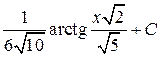 ;
;
37. 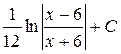 ; 38.
; 38. 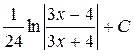 ; 39.
; 39. 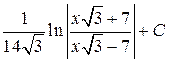 ;
;
40. 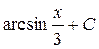 ; 41.
; 41. 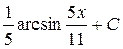 ; 42.
; 42. 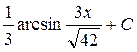 ; 43.
; 43. 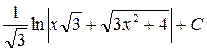 ; 44.
; 44. 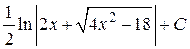 ; 45.
; 45. 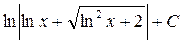 ; 46.
; 46. 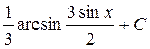 ; 47.
; 47. 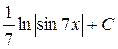 ; 48.
; 48. 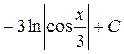 ; 49.
; 49. 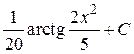 ; 50.
; 50. 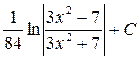 .
.
Дата добавления: 2017-01-08; просмотров: 1524;











