ИНТЕГРИРОВАНИЕ ДРОБНО-РАЦИОНАЛЬНЫХ ФУНКЦИЙ.
Рассмотрим интегралы от важного класса дробно-рациональных функций вида
.
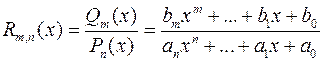Если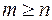 
, рациональную функцию называют неправильной и называют правильной при 
.
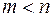При интегрировании рациональных функций применяют преобразования:
1. Неправильную рациональную функцию представляют, например, путем деления уголком в виде суммы многочлена степени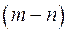 
и правильной рациональной функции. Эта операция называется выделением целой части.
2. Правильная рациональная функция представляется в виде суммы элементарных дробей вида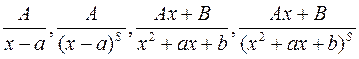 
, где квадратный трехчлен 
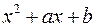не имеет действительных корней. Такое представление делается после разложения знаменателя на множители.
В конечном итоге интеграл от рациональной функции сводится к сумме интегралов от элементарных дробей и многочлена.
Схема разложения дроби на простейшие.
1. В разложение знаменателя входят только множители первой степени и ни один из них не повторяется. Тогда:
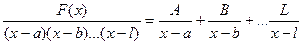
A,B,…L находятся по методу неопределенных коэффициентов:
1) Освобождаются от знаменателей.
2) Приравнивают коэффициенты при одинаковых степенях x в правой и левой частях. Получается система 1 степени.
3) Решается система, она имеет единственное решение.
2. В разложении знаменателя входят только множители первой степени и некоторые из них повторяются k раз.
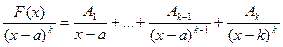
3. В разложении знаменателя входят множители 2 степени (не разложимые на действительные многочлены 1 степени), и не один из них не повторяется. Тогда в разложении дроби каждому множителю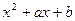 
соответствует простейшая дробь 
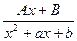. Множителям первой степени (если они есть) соответствует простейшие дроби типа 
.
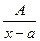4. В разложении знаменателя входят множители 2 степени (не разложимые на действительные многочлены 1 степени), и некоторые из них не повторяется. Тогда в разложении дроби каждому множителю 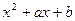, повторяющемуся k раз, соответствует сумма простейших дробей вида:
.
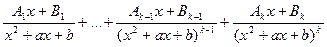Примеры.
Выделить целую часть рациональной функции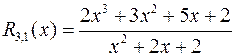 
и выполнить интегрирование.
Делаем деление уголком по следующей схеме до тех пор, пока степень остатка не станет меньше степени знаменателя:
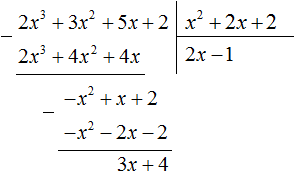
Результат деления имеет вид
.
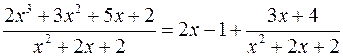Многочлен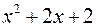 
не имеет действительных корней, поэтому разложение получившейся правильной рациональной функции невозможно и приступаем к интегрированию.
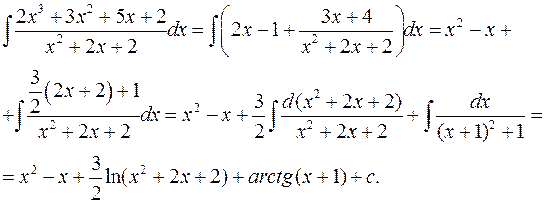
Пример.
Разложить на множители многочлены: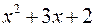 
, 
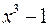и 
.
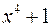Для разложения многочлена на множители в общем случае необходимо найти его корни. Поэтому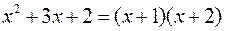 
. Полезно воспользоваться известными формулами или применить искусственный прием:
,
.
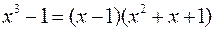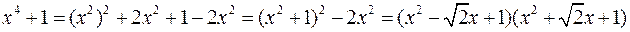Пример.
Разложить на элементарные дроби и проинтегрировать функци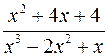и
и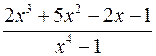 
.
Разлагаем знаменатель на множители
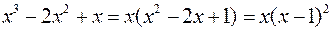
и по виду знаменателя записываем искомое разложение
.
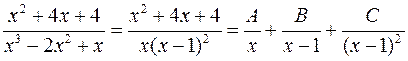Коэффициенты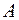 
, 
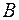и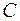 
находим из равенства 
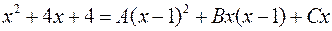, приравнивая коэффициенты при одинаковых степенях 
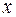слева и справа. Получим систему
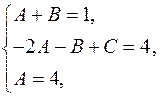
откуда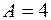 
, 
, 
.
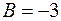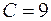Интегрируя сумму элементарных дробей с учетом найденных коэффициентов, приходим к результату
.
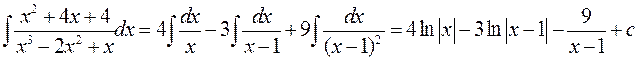Разложение на элементарные дроби функции 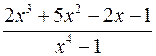проводим в аналогичной последовательности.
,
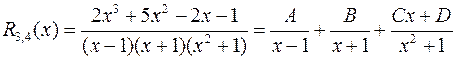где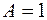 
, 
, 
, 
;
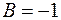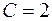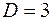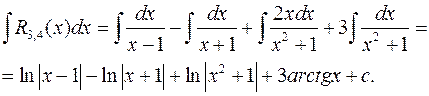
Пример.
Найт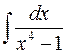и 
и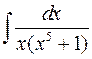 
.
В некоторых случаях использование специальных приемов позволяет избежать трудоемких преобразований, свойственных общей схеме. Например, в задачах этого номера преобразования можно выполнить следующим образом:
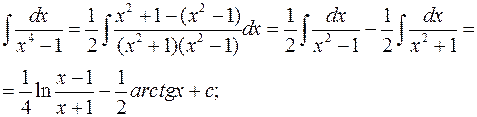
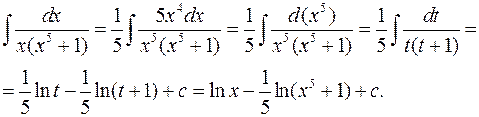
Общая схема интегрирования дробных рациональных функций
- выделение целой части функции, в результате которого получается представление рациональной дроби в виде суммы многочлена и правильной дроби;
- разложение правильной дроби на сумму простейших дробей;
- нахождение интегралов от простейших рациональных дробей и суммирование результатов.
Дата добавления: 2017-03-12; просмотров: 4965;
Поиск по сайту
Узнать еще
- А. Модели экономического прогноза на базе производственных функций.
- Безусловнорефлекторные, условнорефлекторные, гуморальные механизмы регуляции половых функций.
- Ввод и редактирование формул. Обзор функций.
- Виды выходных функций.
- Вычисление Z-передаточных функций.
- Графическое и численное интегрирование.
- Дифференциальные уравнения равновесия жидкости и их интегрирование для простейшего случая
- Интегралы от дробно-рациональных выражений
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по географии
Публикации по медицине
