Дифференциальные уравнения равновесия жидкости и их интегрирование для простейшего случая

Получим дифференциальные уравнения равновесия жидкости в общем случае, когда на нее действуют не только сила тяжести, но и другие массовые силы, например, силы инерции переносного дви­жения при так называемом относительном покое. В неподвижной жидкости возьмем произвольную точку М с координатами 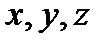и давлением р. Систему координат будем считать жестко связанной с сосудом, содержащим жидкость. Выделим в жидкости элементарный объем в форме прямоугольного параллелепипеда с ребрами, параллель­ными координатным осям и соответственно равными 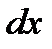, 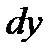и . 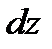Пусть точка М будет одной из вершин параллелепипеда. Рассмотрим условия равновесия выделенного объема жидкости. Пусть внутри параллелепипеда на жидкость действует равнодействующая массовая сила, составляющие которой, отнесенные к единице массы , равны 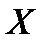, 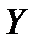и 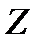. Тогда массовые силы, действующие на выделенный объем в направлении координатных осей, будут равны этим составляющим, умноженным на массу выделенного объема.

Давление 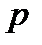есть функция координат 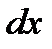, 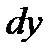и 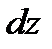., но вблизи точки М по всем трем граням параллелепипеда оно одинаково, что вытекает из доказанного выше свойства гидростатического давления .При переходе от точки М, например, к точке N изменяется лишь координата 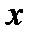на бесконечно малую величину 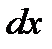, в связи с чем функция 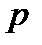получает приращение, равное частному дифференциалу 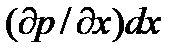, поэтому давление в точке N равно

,

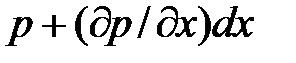где 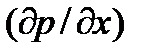— градиент давления вблизи точки М в направлении оси .

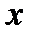Рассматривая давления в других соответствующих точках граней, нормальных к оси 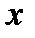видим, что они отличаются на одинаковую (с точностью до бесконечно малых высших порядков) величину.

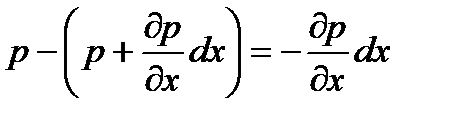
Ввиду этого разность сил давления, действующих на параллелепипед в направлении оси 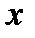, равна указанной величине, умноженной

на площадь грани: .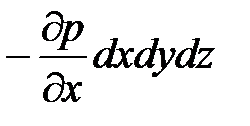

Аналогичным образом, но через градиенты давления 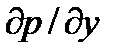и 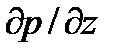выразим разности сил давления, действующие на параллелепипед в направлении двух других осей.

На выделенный параллелепипед действуют лишь указанные массовые силы и силы давления, поэтому уравнения равновесия параллелепипеда в направлениях трех координатных осей запишем в следующем виде:

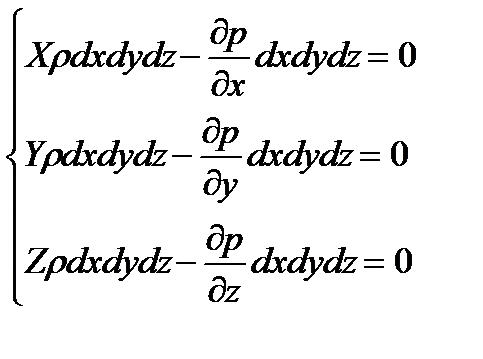(2.4)

Разделим эти уравнения на массу 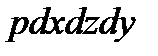параллелепипеда и перейдем к пределу, устремляя 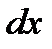, 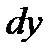и 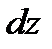., к нулю, т. е. стягивая параллелепипед к исходной точке М. Тогда в пределе получим уравнения равновесия жидкости, отнесенные к точке М:

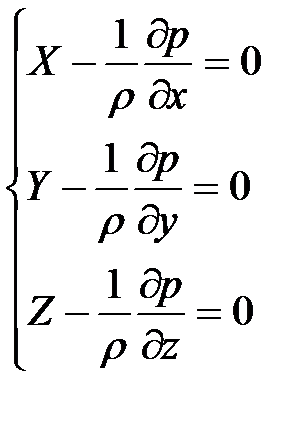(2.5)

Система (2.5) дифференциальных уравнений гидростатики называется уравнениями Эйлера .

Для практического пользования удобнее вместо системы уравнений (2.5) получить одно эквивалентное им уравнение, не содержащее частных производных. Для этого умножим первое из уравнений (2.5) на 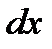, второе на 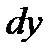, третье на 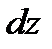и, сложив все три уравнения, получим

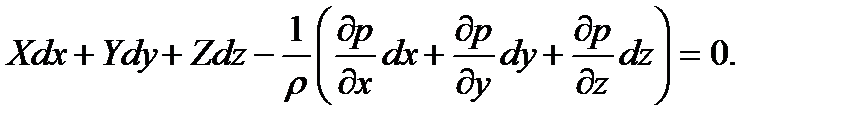
Трехчлен, заключенный в скобках, представляет собой полный дифференциал давления, т. е. функции 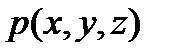, поэтому предыдущее уравнение можно переписать в виде:

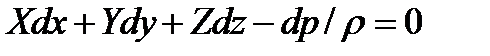
или,

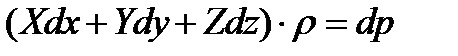(2.6)

Полученное уравнение выражает приращение давления dp при изменении координат на 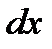, 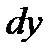и 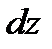., вобщем случае равновесия жидкости.

Если предположить, что на жидкость действует только сила тяжести, и направить ось z вертикально вверх, то X=Y=O, Z=g и, следовательно, вместо уравнения (2.7) для этого част­ного случая равновесия жидкости получим

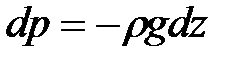(2.7)

После интегрирования будем иметь

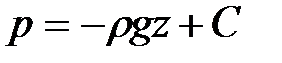
Постоянную интегрирования найдем, подставив параметры свободной поверхности, для которой при z = z₀ p = р₀

Получим

.

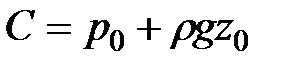При этом

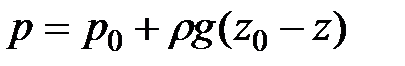(2.8)

или

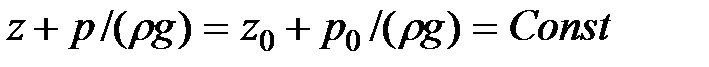
Заменяя в уравнении(2.8) разность 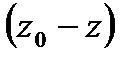на h глубину расположения точки М, найдем

.

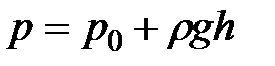Получили то же основное уравнение гидростатики ,которое было выведено в предыдущем параграфе иным путем.