Интегрирование биноминального дифференциала.
Определение: Биноминальным дифференциалом называется выражение вида:
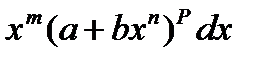 (1),
(1),
где a, b - некоторые вещественные числа. m, n, p - рациональные числа.
Известно три случая интегрирования биноминального дифференциала.
I) p- целое число. Биноминальный дифференциал превращается в дробно-линейную иррациональность, 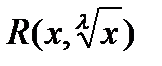 , где
, где 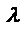 -наименьшее общее кратное знаменателей m и n.
-наименьшее общее кратное знаменателей m и n.
Пример: 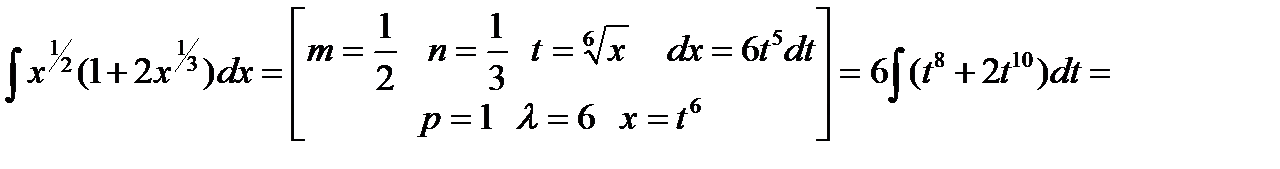
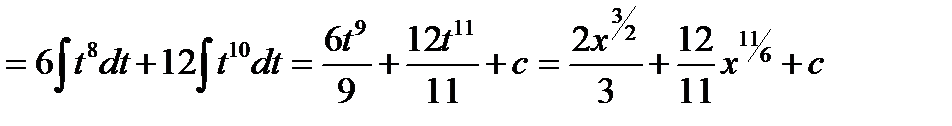
Биноминальный дифференциал (1) всегда может быть представлен в виде:
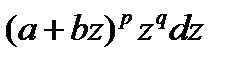 (2)
(2)
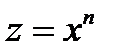 ,
, 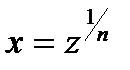 ,
, 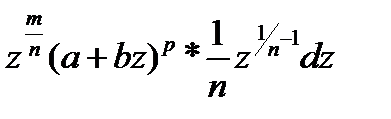
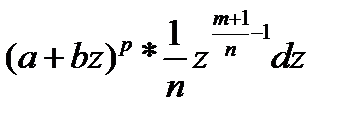 .
.
величину 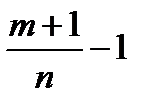 обозначим через
обозначим через 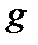 .
.
Из представления (2) следует второй случай интегрируемости биноминального дифференциала. Если 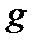 =целому числу то выражение (2) также является дробно-линейной иррациональностью.
=целому числу то выражение (2) также является дробно-линейной иррациональностью.
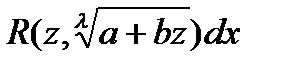 , где
, где 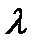 - знаменатель числа p.
- знаменатель числа p.
Если g=целое число, то выражение 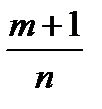 также является целым числом.
также является целым числом.
Второй случай интегрируемости определяется соотношением: 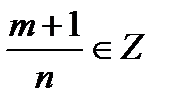 и рационализация осуществляется подстановкой
и рационализация осуществляется подстановкой 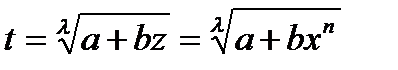
Пример: 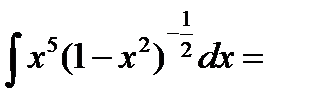
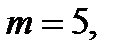 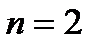
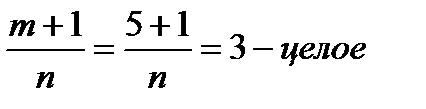
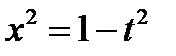 , , 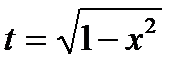 , , 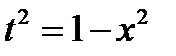 , , 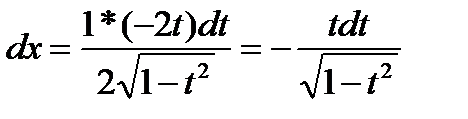
|
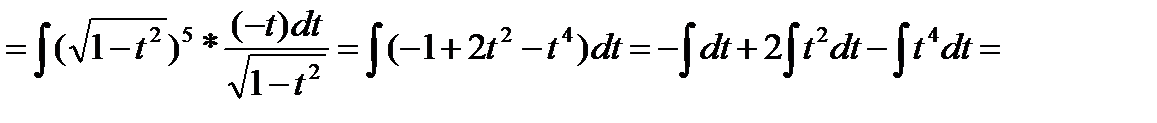
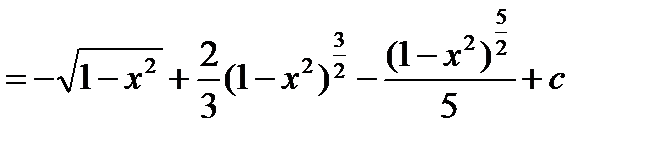
III) Выражение (2) можно представить в виде:
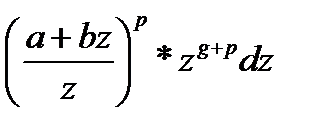 (3)
(3)
Третий случай интегрируемости биноминального дифференциала соответствует целому числу g+p, то есть 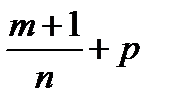 целое число.
целое число.
При этом выражение (3) является дробно линейной иррациональностью вида: 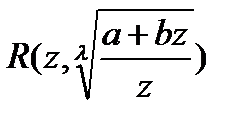 . В этом случае рационализация достигается подстановкой:
. В этом случае рационализация достигается подстановкой: 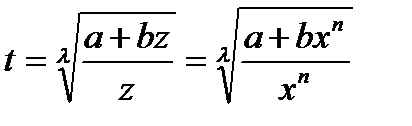 . Таким образом, интеграл от биноминального дифференциала выражается через элементарные функции, если окажется целым одно из чисел.
. Таким образом, интеграл от биноминального дифференциала выражается через элементарные функции, если окажется целым одно из чисел.
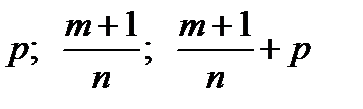
Эти случаи интегрируемости были известны ещё Ньютону, однако в середине позапрошлого века Пафнутий Львович Чебышев (1821-1894), доказал замечательный факт, что других случаев интегрируемости в конечном виде для биноминальных дифференциалов не существует.
Пример: Вычислить интеграл 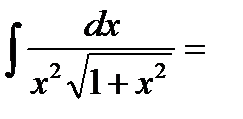
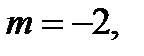 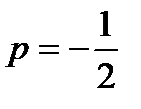 , , 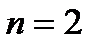
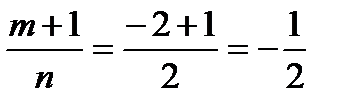 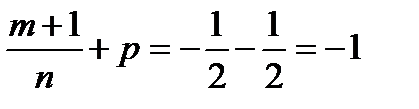
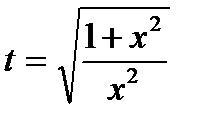 , , 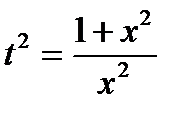 , , 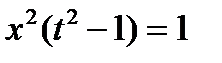 , , 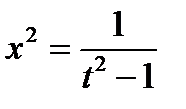 , , 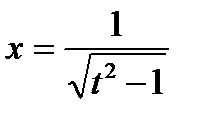 , , 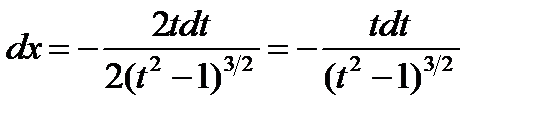
|
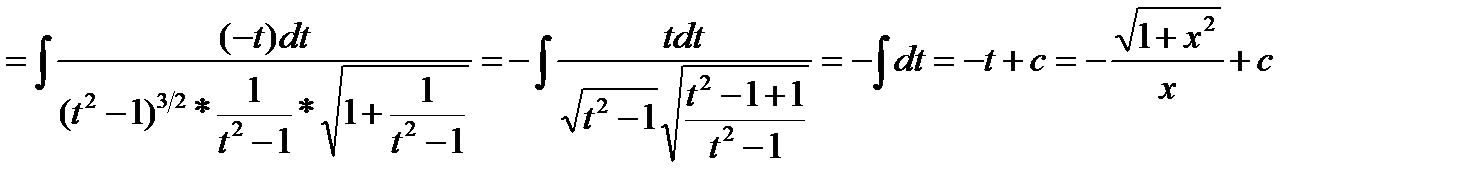
Дата добавления: 2017-06-13; просмотров: 1301;











