Интегрирование дифференциального уравнения линии прогибов и определение произвольных постоянных.

Пример 13.1. Найдем перемещения для балки, загруженной нагрузкой, интенсивность которой изменяется по закону 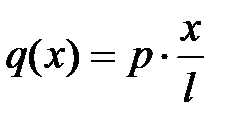(рис.13.2,а).

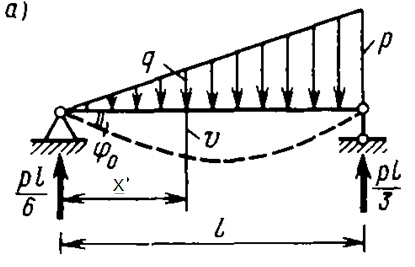
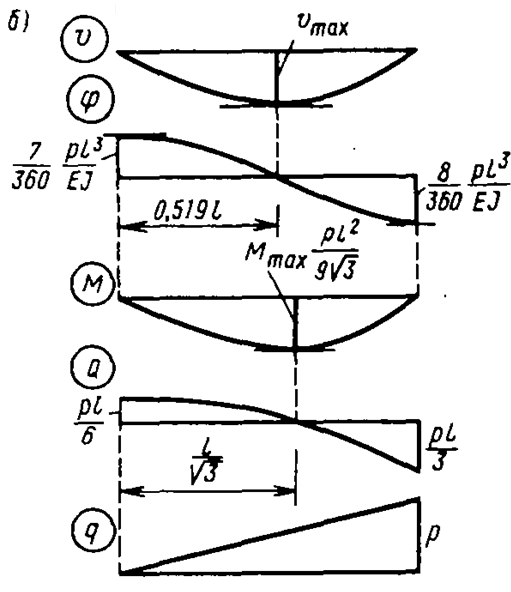
Рис. 13.2 Изгиб шарнирно опертой балки треугольной нагрузкой

Для шарнирно опертой балки (рис. 13.3) воспользуемся дифференциальным уравнением (13.3) и условиями закрепления

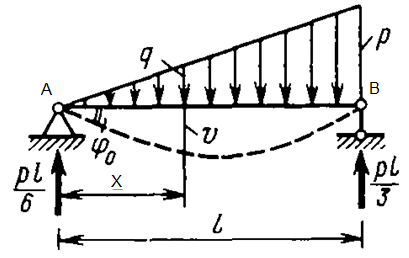
Рис. 13.3

,

.

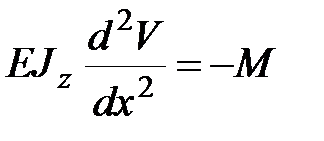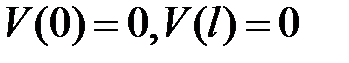Определяем опорные реакции:

,

,

,

,

,

.

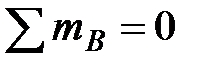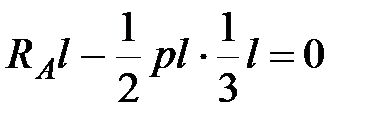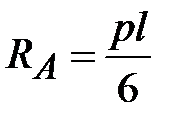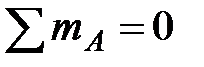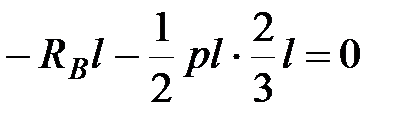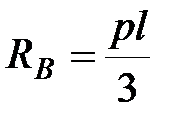В сечении с координатой 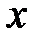выражение для изгибающего момента имеет вид:

,

.

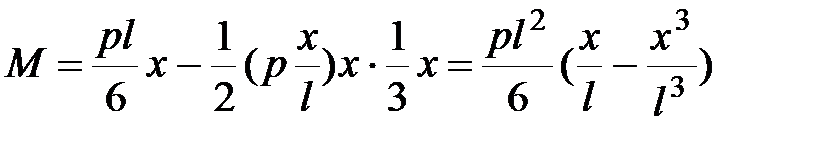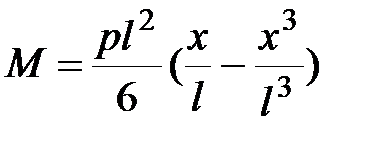(13.8)

Подставляем (13.8) в уравнение (13.3) и интегрируем:

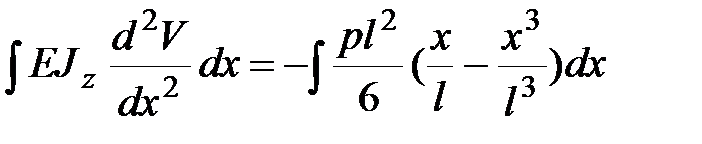
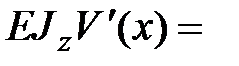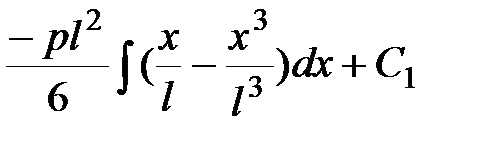
(13.9)

.

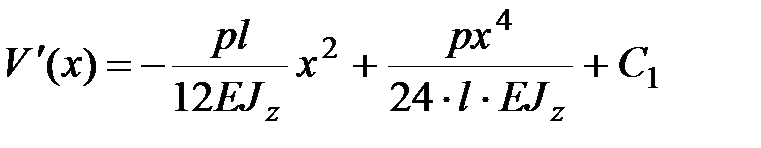(13.10)

Вновь интегрируем обе части уравнения (13.10), получаем:

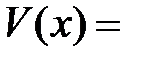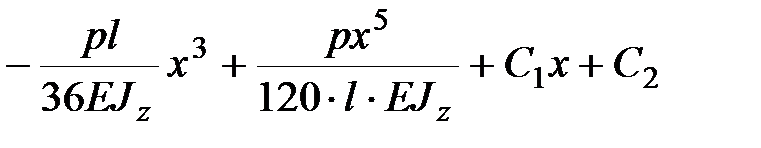
(13.11)

Постоянные интегрирования находим из условий закрепления:

Прогиб на левой опоре равен нулю: , .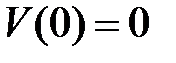

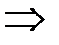
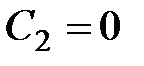Прогиб на правой опоре равен нулю:

, , .

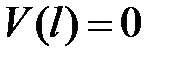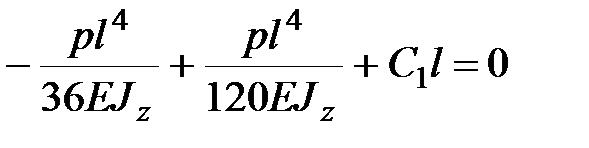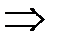
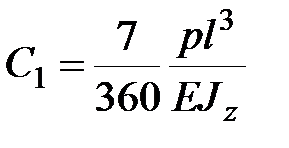Окончательные выражения для искомых функций имеют вид:

, + , , , .

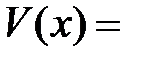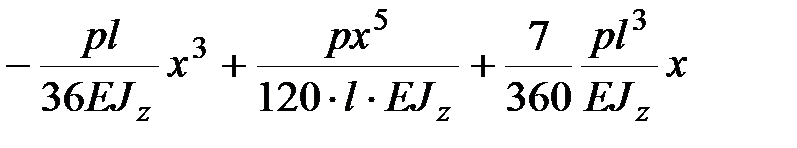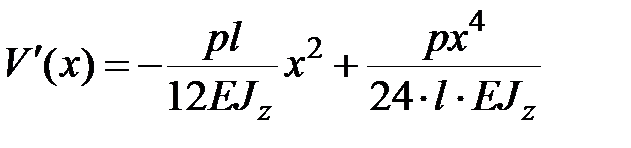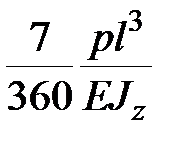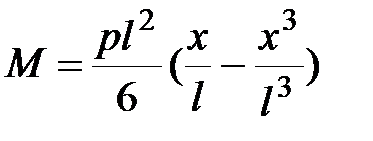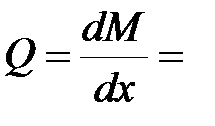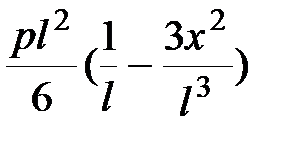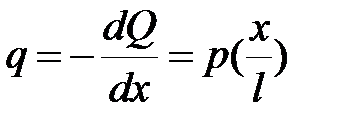(1.12)

Эпюры перемещений, усилий и интенсивности нагрузки показаны на рис. 13.2, б. На эпюрах отмечены точки максимума прогибов и изгибающих моментов.

Пример 13.2 Определить прогибы и внутренние усилия M и Q для статически неопределимой балки (рис.13.4)

В этой балке четыре неизвестных реакции (момент и три силы) и только три уравнения для их определения. Поэтому данная задача относится к статически неопределимым.

Для решения данной задачи воспользуемся системой четырех дифференциальных уравнений

, , , .

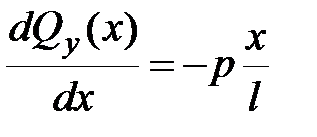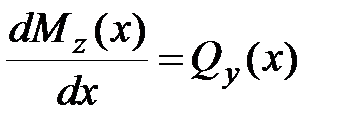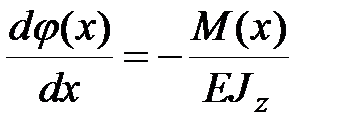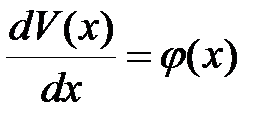(13.13)

Интегрирование системы (13.3) выполним с учетом условий закрепления:

.

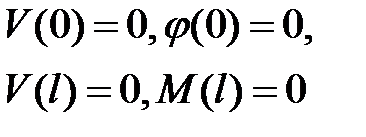(13.14)

Интегрируем первое уравнение системы:

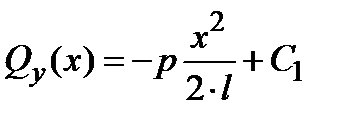
(13.15)

Подставляем (13.15) во второе уравнение системы и интегрируем:

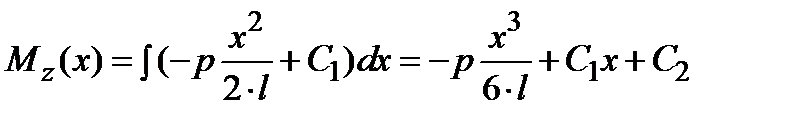
(13.16)

Подставляем (13.16) в третье уравнение системы и интегрируем:

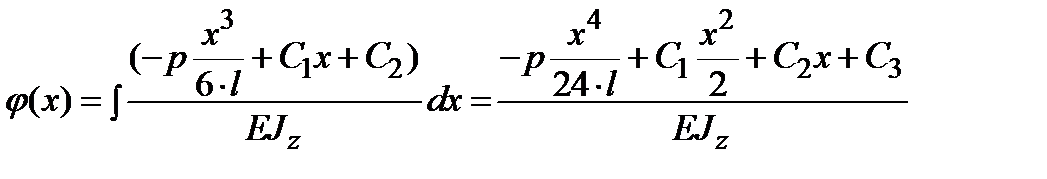
(13.17)

Подставляем (13.17) в четвертое уравнение системы и интегрируем:

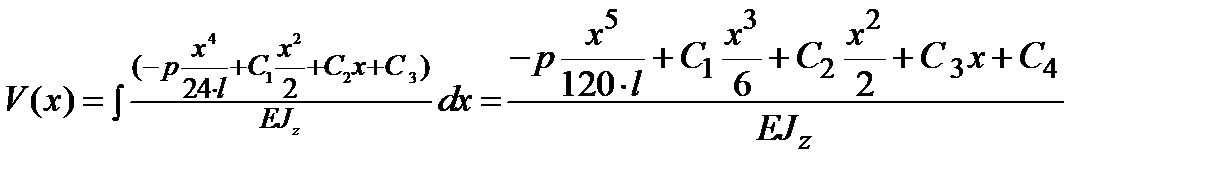
(13.18)

Постоянные интегрирования определяем из условий закрепления:

1) 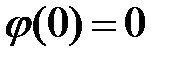, из (13.17) получим .

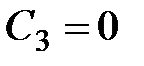2) 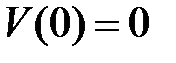, из (13.18) получим .

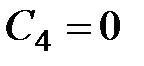3) 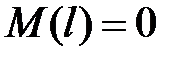, из (13.16) получим: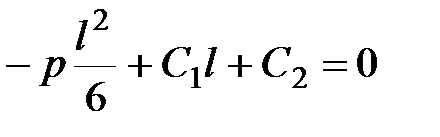

4) 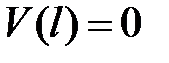, из (13.18) получим: .

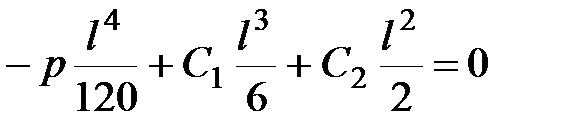Из условий 1-го и 2-го условий вытекает геометрический смысл постоянных интегрирования.

Константа 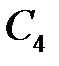пропорциональна прогибу в начале координат, а константа 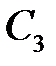углу поворота сечения в начале координат.

Решаем систему уравнений (3-е и 4-е условия):

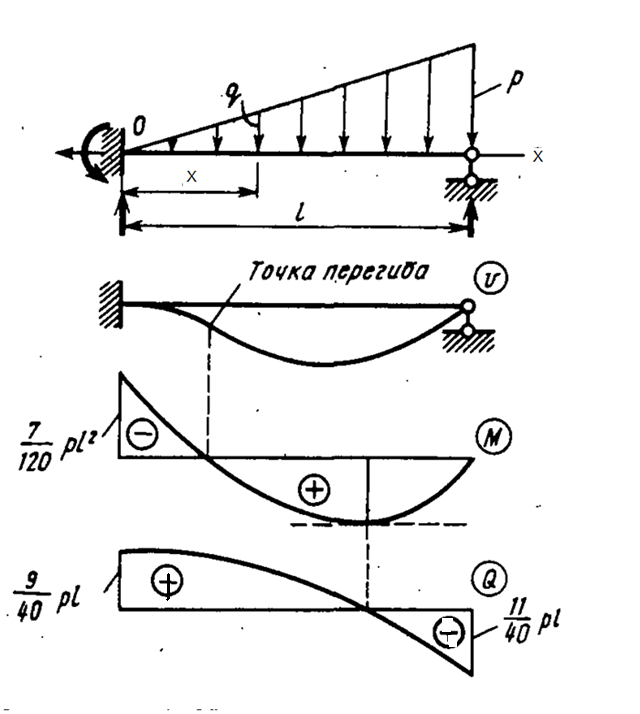Рис. 13.4 Эпюры прогибов, изгибающих моментов и поперечных сил в статически неопределимой балке

, ,

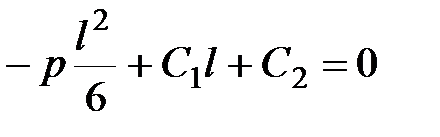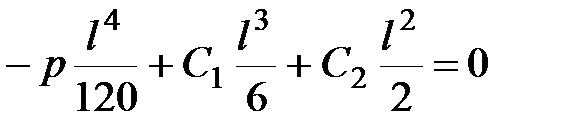(13.19)

Умножаем первое уравнение на 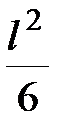и вычитаем из второго, получаем

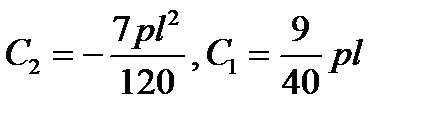
(13.20)

Подстановка констант в уравнения (13.15)-(13.18) дает

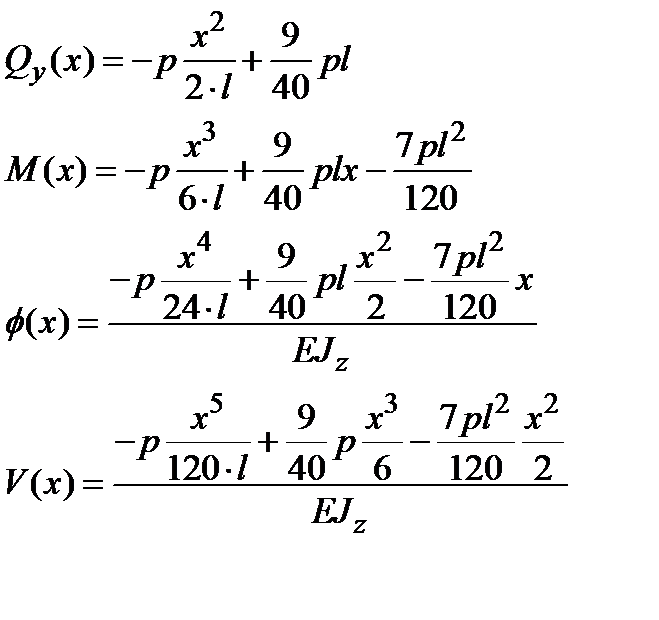
(13.21)

Эпюры перемещений и усилий представлены на рис.13.4.