Определения и свойства неопределенного интеграла

Определение 1. Функция F(x) называется первообразной для функции f(x) на некотором промежутке, если в каждой точке этого промежутка функция F(x) дифференцируема и выполняется равенство F '(x) = f(x).

Если известна одна первообразная F(x) для функции f(x) на интервале (a;b), то любая другая первообразная может быть представлена в виде F(x) + С, где С – произвольная постоянная величина. Такая форма записи первообразных носит название общего вида первообразной.

Геометрически, в системе координат xoy, графики всех первообразных функций от данной функции f(x) представляют семейство кривых, зависящих от одного параметра с, которые получаются одна из другой путем параллельного сдвига вдоль оси oy (рис. 1).

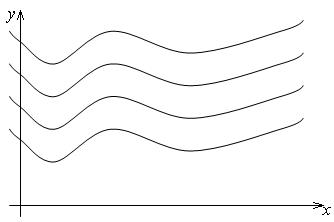
Рис. 1. Семейство первообразных функций

Определение 2. Множество всех первообразных для данной функции f(x) на интервале (a;b) называется неопределённым интегралом функции f(x) на этом интервале и обозначается символом:

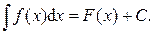
Теорема 1. Если функция f(x) непрерывна на промежутке (a;b), то она имеет на промежутке (a;b) первообразную и неопределённый интеграл.

Из определений первообразной F(x) и неопределённого интеграла от данной функции f(x) на некотором промежутке следуют свойства неопределённого интеграла:

1. .

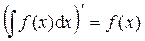2. .

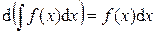3. 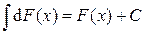, где С – произвольная постоянная.

4. 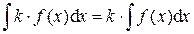, где k = const.

5.

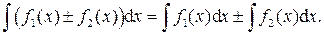
Замечание. Все вышеперечисленные свойства верны при условии, что интегралы, фигурирующие в них, рассматриваются на одном и том же промежутке и существуют.

Таблица основных неопределённых интегралов

1. .

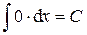2. .

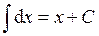3. .

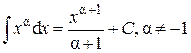4. .

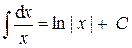5. .

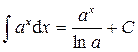6. .

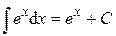7. .

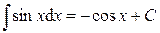8. .

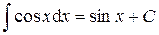9. .

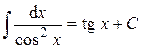10. .

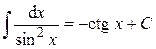11. .

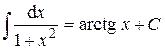12. .

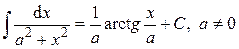13. .

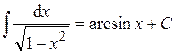14. .

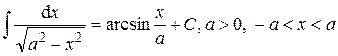15. .

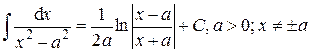16. .

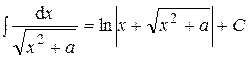В формулах 1–16 С – произвольная постоянная.

Справедливость формул интегрирования, а также и каждый результат интегрирования можно проверить путем дифференцирования на том основании, что интегрирование есть действие обратное дифференцированию.