Модели рядов динамики

Укрупненными составляющими изменения уровней ряда динамики (компонентами динамических рядов) являются: долговременные, кратковременные, случайные колебания и тенденция или тренд.

К долговременным относятся циклические колебания, отражающие конъюнктурные циклы и состоящие в переходе от более или менее благоприятной конъюнктуре к кризису, депрессии и снова оживлению и благоприятной конъюнктуре.

Кратковременные колебания являются сезонными, представляющими собой повторяющиеся из года в год изменения показателя в определенные промежутки времени. Наблюдая их в течение ряда лет для каждого квартала или месяца, можно вычислить соответствующие средние или медианы, которые принимаются за характеристики сезонных колебаний. Например, можно в течение ряда лет наблюдать, на сколько процентов значение показателя в январе отличается от среднегодового и отсюда вычислить среднюю (или медиану), то же сделать для февраля, марта и т.д. Всего 12 таких средних дадут общую характеристику сезонных колебаний.

Сезонные колебания являются результатом влияния природных, общественных и экономических факторов. Сезонные колебания характеризуются длительностью периода колебаний (отрезок времени между соседними точками максимума и минимума), амплитудой (разность между максимальными и минимальными значениями показателя) и размещением максимумов во времени. В зависимости от вида сезонности применяются различные статистические методы для определения сезонных колебаний, например, расчет индексов сезонности, сезонной волны, спектральный анализ.

Случайныеколебания представляют собой разность между фактическими значениями ряда динамики и его выравненными значениями. В некоторых случаях выравненные значения сочетают тренд, циклические колебания и сезонные колебания.

Тренд – это изменение, определяющее общее направление развития, основную тенденцию рядов динамики. Для выявления тренда используются различные способы выравнивания (сглаживания) ряда, при этом уровни ряда выражаются в виде функции ряда. К наиболее употребительным способам выравнивания относятся: метод скользящих средних; выравнивание с помощью среднего прироста; аналитическое выравнивание по линейной функции, по многочленам различной степени и т.д. с использованием метода наименьших квадратов.

Одним из наиболее распространенных видов тренда в экономических исследованиях является линейный тренд ( рис.3.1) вида

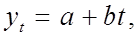
где t – время; a и b – параметры, которые находятся, как правило, методом наименьших квадратов.

Параметр b определяет средний абсолютный прирост ряда динамики.

Степенной тренд – тренд вида (рис.3.2)

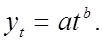
Параметры a и b определяются из линейной регрессии после логарифмирования степенного тренда

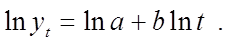
С помощью степенного тренда можно выравнивать временные ряды с разной степенью роста: b > 1 – степень роста выше, чем у линейного тренда, b < 1 – степень роста ниже, чем у линейного.

Экспоненциальный тренд

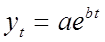
широко используется в экономических исследованиях. Параметр b соответствует среднегодовому темпу прироста ряда динамики. Для оценивания параметров экспоненциального тренда необходимо перейти к логарифмам

Рис.3.1. Линейный тренд

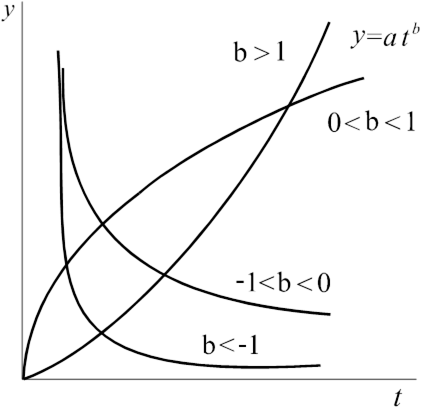
Рис.3.2. Степенной тренд

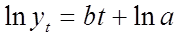
и применить метод наименьших квадратов.

При анализе рядов динамики используются также и другие виды трендов, вид которых приведен на рис.3.3–3.8.

Оценкой колеблемости ряда динамики служит отклонение уровней ряда динамики от их средней величины или от сглаженных значений. Мерой колеблемости является среднее квадратическое отклонение. Если ряд стабилен, то степень колеблемости ряда динамики определяется по формуле

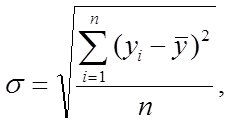
где 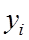– уровень ряда динамики; 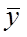– средний уровень ряда; n – число уровней ряда.

При заметно выраженном росте или падении уровней ряда показатель колеблемости ряда динамики рассчитывается по формуле

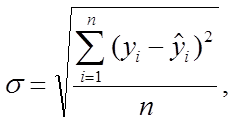
где 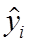– сглаженные (выравненные, теоретические) значения уровней ряда динамики.