ПОКАЗАТЕЛИ ВАРИАЦИИ

Вариация - колеблемость, изменение величины признака в статистической совокупности, т.е. принятие единицами совокупности или их группами разных значений признака. Например, колеблемость заработной платы у рабочих предприятия. Вариация является следствием действия на единицы совокупности множества различных факторов (причин). Вариация измеряется и характеризуется системой показателей вариации. Если признак - принимает одно из двух противоположных значений, то вариация называется альтернативной (например, человек состоит в браке - не состоит). При измерении такой вариации значения признака обозначаются 1 и 0. Если вариация (изменение) признака идет в определенном направлении (но изменение не обусловлено внутренним законом развития явления), то ее называют систематической, если же вариация не имеет явно выраженного направления - случайной.

Вариантом (вариантой) называется значение признака у единицы совокупности, отличное от значений этого признака у других единиц. Некоторые единицы могут иметь одинаковое значение (один и тот же вариант) признака.

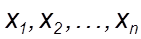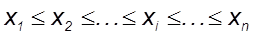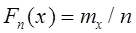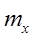Вариационный ряд- расположение значений случайной выборки ( ) с функцией распределения F(x) в порядке их возрастания: , где i -й член вариационного ряда называется i -й порядковой статистикой, а номер члена вариационного ряда - рангом, порядком. Вариационный ряд служит для построения эмпирической (опытной) функции распределения , где - число членов ряда, меньших .

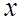Вариационные ряды находят широкое применение при первичной обработке статистических данных, в частности при сравнении уровней показателей объектов (отраслей, предприятий и т.п.).

Показатели вариации - показатели, отображающие размеры вариации (степень колеблемости) признака. К ним относятся: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, средний квадрат отклонений (дисперсия), коэффициент вариации, коэффициент детерминации, эмпирическое корреляционное отношение.

Размах вариации (R) характеризует пределы колеблемости (вариацию) индивидуальных значений ( или вариантов) признака ( x ) в статистической совокупности (или в вариационном ряду) и представляет собой разность между наибольшим ( 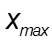) и наименьшим ( 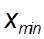) значениями признака, т.е.

,

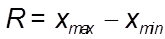Размах вариации вычисляется в тех же единицах измерения, что и признак, вариацию которого он характеризует.

Среднее линейное отклонение ( 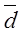) представляет собой среднее значение отклонений вариантов признака от их средней величины. Так как алгебраическая сумма этих отклонений равна нулю, то для вычисления среднего линейного отклонения все отклонения берутся без учета знака. Среднее линейное отклонение вычисляется по формуле :

средней арифметической взвешенной

;

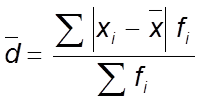или средней арифметической простой (невзвешенной)

,

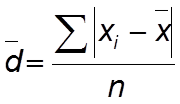где 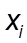- варианты признака;

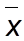- средняя величина признака;

f - веса признаков;

n - численность единиц совокупности.

Среднее квадратическое отклонение ( 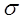) представляет собой корень второй степени из среднего квадрата отклонений значений (вариантов) признака от их средней величины. Имеет ту же размерность, что и признак, для которого оно вычисляется. В математической статистике среднее квадрати-ческое отклонение называется характеристикой рассеяния случайной величины.

Среднее квадратическое отклонение в статистике используется как мера вариации, на его основе вычисляется коэффициент вариации. Среднее квадратическое отклонение рассчитывается по формуле взвешенной:

,

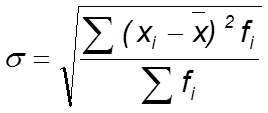или невзвешенной

,

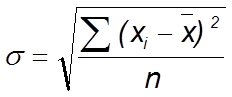где 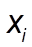- i-е значение признака x ;

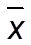- средняя величина признака x ;

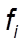- веса вариант;

n - число членов совокупности.

Среднее квадратическое отклонение может быть рассчитано по следующим формулам:

,

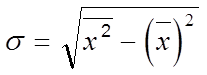где 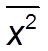- средний квадрат значений признака (средняя величина из

квадратов значений признака);

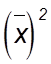- квадрат средней величины признака,

или

,

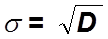где D - дисперсия случайной величины.

Дисперсия в зависимости от вида статистической совокупности может быть генеральной и выборочной.

Генеральная дисперсия - математическое ожидание квадрата отклонения случайной величины от ее математического ожидания или средний квадрат отклонения признака от его среднего значения в генеральной совокупности.

Выборочная дисперсия - смещенная оценка генеральной дисперсии или среднее арифметическое (выборочное среднее) квадрата отклонения наблюдаемых значений признака от их среднего арифметического. Выборочная дисперсия является состоятельной оценкой генеральной дисперсии.

Для сгруппированного вариационного ряда выборочная дисперсия определяется по формуле

,

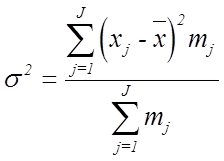где J - число групп;

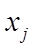- значение признака в j - й группе;

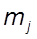- частота признака в j - й группе.

При анализе информации статистической совокупности, разбитой на группы рассчитываются следующие дисперсии: групповая, межгрупповая, внутригрупповая и общая.

Групповая дисперсия (частная) - средний квадрат отклонений значения признака единиц совокупности в группе от их средней величины. Группа является составной частью статистической совокупности. Эта дисперсия характеризует вариацию признака в группе, обусловленную действием на него всех прочих факторов, кроме признака, положенного в основание группировки (группировочного признака). Вычисляется по формулам:

средней взвешенной арифметической

,

или средней арифметической невзвешенной

,

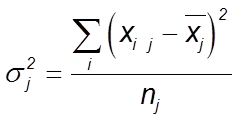где 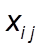- значение признака i -й единицы j -й группы;

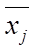- частная (групповая) средняя величина признака в j -й группе;

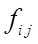- вес значения признака i -й единицы в j -й группе;

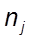- численность единиц j -й группы.

Межгрупповая дисперсия (дисперсия групповых средних) - средний квадрат отклонений средних величин признака в каждой группе, называемых средней групповой (частной), от средней общей для всей статистической совокупности в целом. Межгрупповая дисперсия вычисляется по формуле

,

где 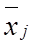- средняя j -й группы;

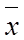- общая средняя;

- вес j -й группы, представляющий собой численность единиц в j -й группе или их долю в численности единиц всей статистической

совокупности в целом;

J - количество групп.

Межгрупповая дисперсия измеряет степень колеблемости (вариацию) признака во всей статистической совокупности за счет фактора, положенного в основание группировки (группировочного признака).

Внутригрупповая дисперсия (средняя дисперсия из групповых дисперсий) - дисперсия, вычисляемая как средняя арифметическая взвешенная из дисперсий, рассчитанных по каждой группе, на которые разбита статистическая совокупность. Определяется по формуле

,

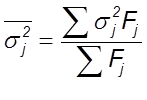где 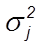- групповая (частная) дисперсия j -й группы.

Внутригрупповая дисперсия измеряет степень колеблемости (вариацию) признака во всей совокупности в целом за счет действия на него всех прочих факторов (признаков), кроме положенного в основание группировки, т.е. группировочного признака.

Общая дисперсия - дисперсия, вычисленная для всей статистической совокупности в целом как средний квадрат отклонений значений признака от общей средней. Измеряет степень колеблемости признака, порождаемую всей совокупностью действующих на него факторов. Может быть вычислена как сумма внутригрупповой и межгрупповой дисперсий

.

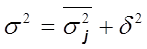Коэффициент вариации является относительной мерой вариации и представляет собой отношение среднего квадратического отклонения к средней величине варьирующего признака, вычисляется по формуле

,

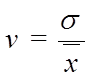где 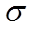- среднее квадратическое отклонение;

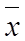- средняя величина признака.

Коэффициент вариации выражается обычно в процентах и дает представление о степени однородности статистической совокупности. Чем меньше величина коэффициента вариации, тем меньше варианты признака отличаются один от другого по величине, и, следовательно, тем однороднее статистическая совокупность. Коэффициент вариации является относительной величиной, абстрагирует различия абсолютных величин вариации разных признаков и дает возможность ее сравнения.

Коэффициент детерминации - представляет собой отношение межгрупповой дисперсии к общей дисперсии и показывает, какую часть общей вариации изучаемого признака составляет межгрупповая вариация, т.е. обусловленная группировочным признаком. Определяется следующим образом

.

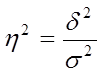Эмпирическое корреляционное отношение - показатель тесноты связи между взаимосвязанными явлениями (их признаками). Расчет эмпири-ческого корреляционного отношения может быть произведен по одной из следующих формул:

,

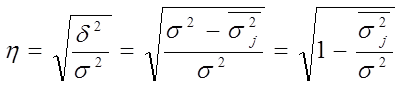где 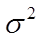- общая дисперсия результативного признака;

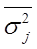- внутригрупповая (средняя из групповых) дисперсия резуль-

тативного признака;

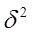- межгрупповая дисперсия результативного признака.

Эмпирическое корреляционное отношение обычно выражается в долях единицы. По абсолютной величине эмпирического корреляционного отношения судят о тесноте связи или степени зависимости результативного признака от одного факторного признака (фактора) или нескольких. Эмпирическое корреляционное отношение может иметь значение от 0 до 1 (с учетом алгебраического знака от “-” до “+”). Знак указывает лишь на характер, направление связи. Если с увеличением (уменьшением) значений факторного признака значения результативного признака также увеличиваются (уменьшаются), то такого рода связь называется прямой и эмпирическое корреляционное отношение берется со знаком “+”, в противном случае связь называется обратной и берется знак “-”. Чем ближе величина эмпирического корреляционного отношения к единице, тем теснее связь.

8. МОДЕЛИ ДИНАМИЧЕСКИХ ПРОЦЕССОВ