А. Аналитические модели.

Они позволяют решать оптимизационные задачи и получать в явном виде соотношения между состояниями ОД, диагностируемыми параметрами и показателями качества систем управления. Это метод малого параметра и метод функции чувствительности. Для функции чувствительности надо иметь передаточную функцию САУ: Ф(р)=F(к₁, к₂, …, к_n, р), где к₁-к_n – входные (собственные параметры ОД). Под функцией чувствительности понимают

.

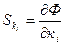
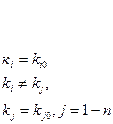Нижний подиндекс 0 указывает на номинальное значение параметра.

(*) Если заменить дифференциальный оператор р на jω, то

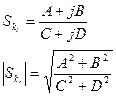
где А=f₁(к₁, …, к_n, ω)

- - - - - - - - - - - - - -

D=f₄(к₁, …, к_n, ω)

Есть два подхода в использовании функции чувствительности:

2. Частотный подход /начиная с (*)/

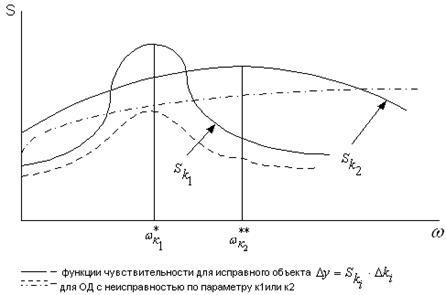
Рис. 4

При изменении параметра схемы к_i (при ω*=const) следят за тем, чтобы Δy контролируемого ОД было меньше либо равно Δy исправного ОД.

2. Назначение равных классов допусков.

При этом находят связь между относительным изменением выходного параметра у и относительными изменениями входных параметров ОД.

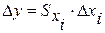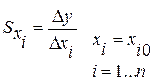
, где . (1)

Выполнив несложные преобразования, получим соотношение, связывающие относительное изменение входного параметра х_i с относительным значением выходного параметра у.

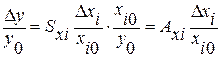, (2)

Тогда

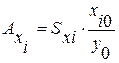, (3)

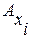- коэффициент влияния i-го параметра.

По (3) можно найти максимальные допуски 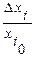на параметры схемы 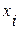, если предварительно вычислить коэффициенты влияния 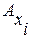(отношение 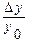задается заказчиком).

В реальных условиях изменяются значения всех параметров схемы (технологический разброс, внешние воздействия и т.д.), поэтому назначают один допуск на все пассивные и активные элементы схемы, используя соотношение по методу равных классов допусков. При этом

.

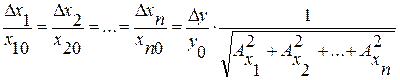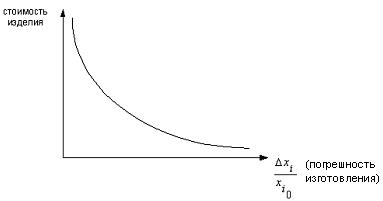
Рис. 5

На рис. 5 представлена зависимость стоимости изделия от точности его изготовления.

Другим видом аналитической модели является корневой годограф, т.е. динамическое распределение корней характеристического уравнения при вариации внутренних параметров схемы. При этом корни характеристического уравнения должны оставаться в левой полуплоскости (комплексной плоскости) UjV и выполнятся условия обеспечения заданного запаса устойчивости как по модулю, так и по фазе.

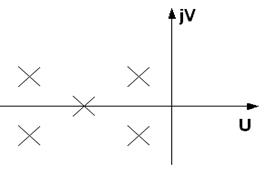
Рис.6