Характеристики рядов динамики

Для изучения изменения явлений во времени в рядах динамики рассчитываются следующие характеристики: средняя хронологическая величина;

абсолютные приросты; темпы роста; темпы прироста; абсолютное значение одного процента прироста; индексы сезонности.

Средняя хронологическая представляет собой среднюю величину из уровней ряда динамики. Вычисляется для интервальных и моментных рядов. Она может быть средней невзвешенной (простой ) и средней взвешенной. Средняя невзвешенная определяется для рядов с равноотстоящими уровнями, взвешенная – для рядов с неравноотстоящими уровнями.

Средняя хронологическая невзвешенная для интервального ряда рассчитывается следующим образом (рис.3.1,а):

а)

y₂ y₃

Уровни ряда, y₁ y₄

y

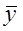
t₁ t₂ t₃ t₄ Время, t

б)

y₂

Уровни ряда, y₁ y₃ y₄

y

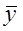
t₁ t₂ t₃ Время, t

в)

y₂ y₃

Уровни ряда, y₁ y₄

y

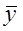
t₁ t₂ t₃ t₄ Время, t

г)

y₂ y₃

Уровни ряда, y₁ y₄

y

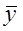
t₁ t₂ t₃ Время, t

Рис.3.1. Средняя хронологическая ряда динамики:

а) интервального полного ряда; б) моментного полного ряда;

в) интервального неполного ряда; г) моментного неполного ряда

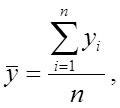
где 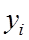– уровень ряда, сохраняющий свое значение в течение периода времени t_i; n – число уровней ряда.

Средняя хронологическая невзвешенная для моментного ряда, представленного на рис.3.1,б :

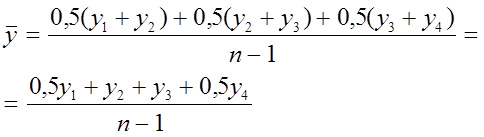
или в общем виде

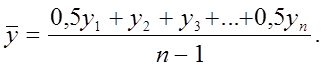
Средняя хронологическая взвешенная для интервального ряда (рис.3.1,в) рассчитывается по формуле

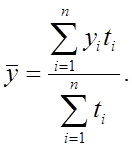
Средняя хронологическая взвешенная для моментного ряда (рис.3.1,г) рассчитывается

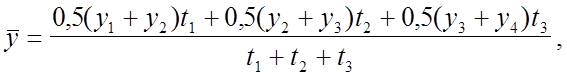
в общем виде

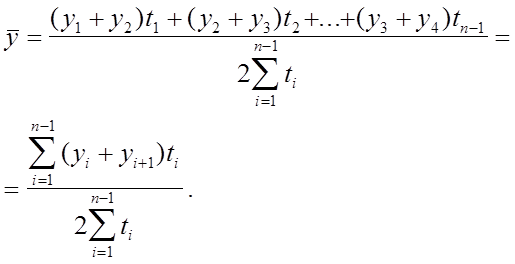
Абсолютный прирост представляет собой разность двух уровней ряда динамики. Абсолютный прирост характеризует скорость (в абсолютном выражении) изменения уровней ряда динамики в единицу времени. Сравниваемый уровень называется текущим, а уровень, с которым производится сравнение – базисным.

Если производится сравнение каждого данного уровня ( 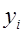) с непосредственно ему предшествующим ( 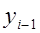), то получаются цепные абсолютные приросты:

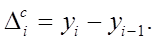
Если каждый уровень ( 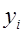) сравнивается с начальным ( 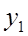) или каким–либо другим, принятым за постоянную базу сравнения ( 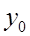), то получаются базисные абсолютные приросты

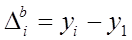или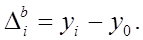

Сумма цепных приростов за определенный период времени равна базисному абсолютному приросту за весь этот период или равна разности между конечным и начальным уровнями ряда динамики:

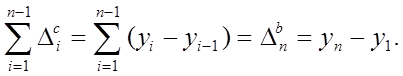
Обобщающим показателем скорости абсолютного изменения уровней ряда является средний абсолютный прирост

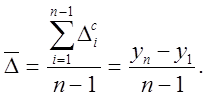
Темп роста – относительный показатель динамики, выражаемый в коэффициентах или в процентах. Представляет собой отношение двух уровней ряда динамики. Темп роста показывает, во сколько раз больше или сколько процентов данный уровень составляет по отношению к другому уровню, принятому за базу сравнения. В качестве базы сравнения для каждого данного уровня может приниматься какой–либо один постоянный уровень (чаще всего начальный уровень ряда) либо непосредственно предшествующий данному уровню. Таким образом, темпы роста могут быть вычислены с постоянной и переменной базой сравнения. Первые называются базисными ( 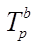), вторые – цепными ( 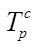). Темп роста характеризует интенсивность изменения величины

ны уровня ряда динамики в единицу времени. Цепные и базисные темпы роста вычисляются по формулам

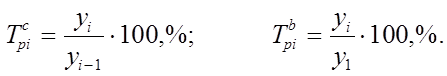
Обобщающим показателем темпа роста уровней ряда динамики служит их средняя величина, называемая средним темпом роста ( 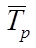). Средний темп роста показывает, как в среднем изменились уровни ряда динамики на протяжении исследуемого периода, он рассчитывается по формуле

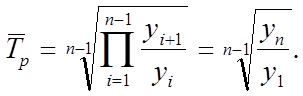
Темп прироста – относительный показатель динамики, представляющий собой отношение абсолютного прироста к уровню динамики, по сравнению с которым он рассчитан. Темп прироста обычно выражается в процентах. Для ряда динамики темпы прироста могут быть вычислены с переменной базой сравнения, они называются цепными ( 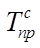), и с постоянной – называются базисными ( 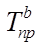). Они рассчитываются следующим образом:

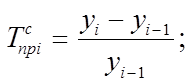
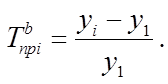
Темпы прироста могут быть определены и как разность между темпом роста, выраженном в процентах, и 100%, т.е.

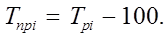
Обобщающим показателем темпов прироста уровней ряда динамики служит их средняя величина, называемая средним темпом прироста. Он обычно вычисляется как разность между средним темпом роста и 100%. Средний темп прироста показывает, как в среднем (например, на сколько процентов) изменялся уровень ряда на протяжении исследуемого периода.

Абсолютное значение одного процента прироста представляет собой отношение абсолютного прироста к темпу прироста, выраженному в процентах. Показывает, какая абсолютная величина показателя приходится на один процент прироста. Абсолютное значение одного процента прироста рассчитывается по формуле

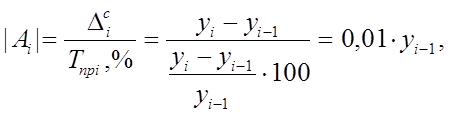
т.е. количественно абсолютное значение одного процента прироста равно одной сотой части базисного уровня.

Индексы сезонностиявляются показателями интенсивности сезонных колебаний. В общем виде определяются как отношение каждого уровня ряда динамики в виде помесячных (реже поквартальных) данных к теоретическому или среднему уровню, принимаемому в качестве базы сравнения. Индексы сезонности обычно выражаются в процентах. Формулы расчета индексов сезонности следующие:

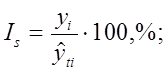
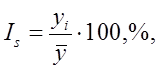
где y_i – фактические уровни ряда динамики; 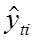– сглаженные (выравненные, теоретические) уровни ряда динамики; 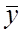– средняя величина из уровней ряда динамики.

Совокупность индексов сезонности представляет собой сезонную волну.

Способы определения индексов сезонности зависят прежде всего от характера основной тенденции ряда динамики. Для нестационарных рядов используется сравнение с теоретическими уровнями, для стационарных – со средним уровнем. Расчет по второй формуле называется способом простых средних. При этом способе средние уровни одноименных месяцев (если помесячные данные взяты за несколько лет) сопоставляются со средним месячным уровнем за весь период, охватываемый рядом. Применяются также способы расчета индексов сезонности на основе метода скользящих средних и аналитического выравнивания.