Относительный покой жидкости.

Относительным покоем называется такое состояние жидкости, при котором отдельные ее частицы не смещаются одна относительно другой, и вся масса жидкости движется как твердое тело (т.е. покой жидкости относительно содержащего ее сосуда, в то время как сам сосуд находится в движении).

Сначала дадим определение поверхности равного давления. Поверхность, проведенную в покоящейся жидкости таким образом, что давление во всех ее точках будет одинаковым, называется поверхностью равного давления. Т.е. p = const и dp = 0, а т.к. 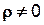, то из (2-9) получим дифференциальное уравнение поверхности равного давления: .

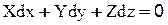Рассмотрим часто встречающийся на практике случай относительного покоя жидкости во вращающихся сосудах (например, в сепараторах и центрифугах) и определим форму поверхности равного давления. При вращении сосуда, находящаяся в нем жидкость вращается вместе с ним с той же, как и сосуд, угловой скоростью w. И жидкость будет находится под действием сил давления, тяжести и центробежной силы, действующей нормально к оси вращения. В результате одновременного действия на жидкость указанных сил, свободная поверхность, бывшая до вращения горизонтальной плоскостью на высоте h от дна сосуда, представится поверхностью вращения. На частицу жидкости действуют объемные силы тяжести G =mg и силы инерции F_И=mw²r , где r - расстояние частицы от оси вращения. Проекции ускорений этих сил на оси координат будут равны: X=w²x; Y=w²y; Z=-g, что приводит к следующему дифференциальному уравнению поверхности равного давления:

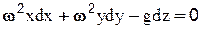. Интегрируя это уравнение, получаем:

Рис.2.11.

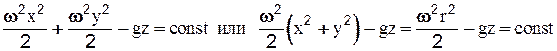
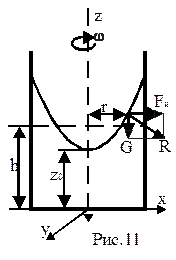
Поверхность равного давления, описываемая данным уравнением, представляет собой параболоиды вращения относительно оси z (которые в сечении вертикальными плоскостями дают параболы, а в горизонтальных плоскостях окружности).

Распределение давления в жидкости может быть получено из основного уравнения равновесия (2-9). Для данного случая 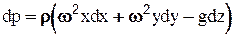, после интегрирования .

Если затем давление в некоторой точке на оси вращения (x=0; y=0; z=z₀) обозначить 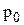и составить для нее уравнение, аналогичное предыдущему, т.е. p₀=-rgz₀+C, определим постоянную интегрирования: C=p₀+rgz₀ ;

тогда 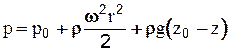. Отсюда видно, что при вращении сосуда давление в жидкости оказывается больше обычного гидростатического давления в неподвижном сосуде и будет тем больше, чем больше радиус и угловая скорость.

Контрольные вопросы

1. Что такое жидкость, какими свойствами она характеризуется?

2. Чем отличается идеальная жидкость от реальной?

3. Что называют гидростатическим давлением, каковы его основные свойства?

4. Каково основное уравнение гидростатики?

5. Что называют абсолютным давлением, избыточным давлением, вакуумом?

6. Сформулируйте закон Паскаля.

7. Как определить силу давления жидкости на плоскую стенку?

8. Как определяются вертикальная и горизонтальная составляющие полной силы гидростатического давления на криволинейную поверхность?

9. Сформулируйте закон Архимеда.

ГИДРОДИНАМИКА

Основная задача гидродинамики - изучение законов движения капельных жидкостей. Исследования в области гидродинамики заключаются преимущественно в нахождении основных величин -скоростей течения и давлений, возникающих в движущейся жидкости. Кроме сил, действующих на покоящуюся жидкость, при движении возникают дополнительно еще силы инерции и трения. В отличие от гидростатического давления, не зависящего от пространственной ориентации площадки, на которую оно действует, гидродинамическое давление благодаря касательным силам различно в направлениях x,y,z. Вязкость жидкости является причиной неравенства скоростей в различных точках одного и того же поперечного сечения движущейся массы жидкости. Установление связи между давлением и скоростью в любой точке движущейся жидкости и в любой момент времени относится к числу основных задач гидродинамики.