Бернулли для струйки идеальной жидкости.

Предположим, что центры тяжести живых сечений струйки 1-1 и 2-2 расположены на высотах z₁ и z₂ от плоскости сравнения 0-0 и что в этих центрах тяжести расположены пьезометрические трубки. Жидкость в каждой трубке поднимется на высоту 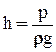,т.е. на пьезометрическую высоту.

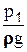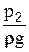Т.е. z₁ и z₂ представляют собой геометрические высоты центров тяжести соответствующих живых сечений струйки над плоскостью сравнения, а члены и пьезометрические высоты, отвечающие давлениям в указанных центрах тяжести. Третий член уравнения 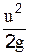имеет ту же размерность, что и два других, т.е. 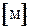и представляет собой скоростную высоту, соответствующую скорости u и называется скоростным или динамическим напором. Отложим от т.А отрезок Аа равный пьезометрической высоте 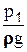, а от т.В - отрезок Вb равный 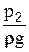. Затем от точек a и b отложим отрезки аа^/ и bb^/, соответствующие скоростным напорам .

Рис.2.17.

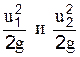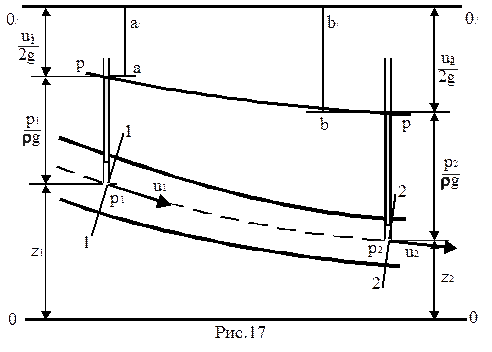
Аналогичные построения можно сделать для ряда живых сечений, взятых вдоль элементарной струйки. Т.к. сумма трех членов 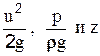для идеальной жидкости постоянна, вдоль оси струйки, то вершины вертикальных отрезков аа^/ и bb^/ располагаются на одинаковых вертикальных расстояниях от плоскости сравнения 0-0, и вершины этих отрезков должны лежать в одной горизонтальной плоскости, называемой напорной плоскостью 0^/-0^/. В случае идеальной жидкости напорная плоскость является горизонтальной. Если плавно соединить уровни жидкости в пьезометрических трубках, то получим пьезометрическую линию p-p.

Сумма трех высот называется полным гидродинамическим напором и обозначается H_Д. Следовательно, полный напор представляет собой сумму потенциального 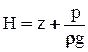и скоростного 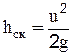напоров, т.е. H_Д=H+h_ск. Все изложенное отражает геометрический смысл уравнения Бернулли.

Выясним физический смысл уравнения Бернулли. Рассмотрим частицу жидкости массой dm, которая движется по линии тока. Определим величину полной энергии, которой обладает частица в сечениях 1-1 и 2-2. Полная энергия представляет собой сумму кинетической и потенциальной энергии. Кинетическая энергия в сечении 1-1 равна 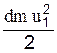. Потенциальная энергия относительно плоскости сравнения 0-0 равна произведению веса частицы на высоту ее подъема над этой плоскостью 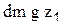. В сечении 1-1 частица будет поднята на высоту 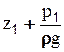, где 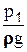- высота, соответствующая давлению, которое поднимет эту частицу, например, в пьезометрической трубке. В сечении 2-2 частица, будет поднята на высоту 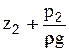. Таким образом, в сечении 1-1 частица обладает потенциальной энергией 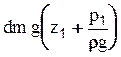. Аналогично в сечении 2-2: 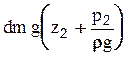. Тогда полная энергия dE в сечениях будет равна:

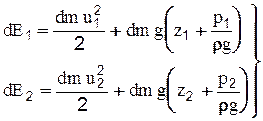(2-35)

Разделив почленно уравнения (2-35) на вес dm g, определим полную энергию жидкости, отнесенную к единице ее веса, т.е. удельную энергию de:

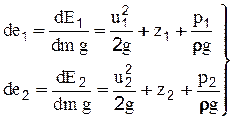(2-36)

здесь: 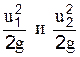- удельная кинетическая энергия; 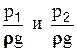- удельная потенциальная энергия давления; 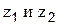- удельная потенциальная энергия положения частицы в сечениях 1-1 и 2-2, соответственно.

Согласно уравнению Бернуллисумма трех указанных величин является постоянной, что приводит к равенству de₁= de₂.

Сечения 1-1 и 2-2 взяты произвольно, поэтому можно записать:

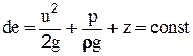(2-37)

Итак, сумма трех членов уравнения Бернулли есть сумма трех удельных энергий: удельной кинетической энергии, удельной потенциальной энергии давления и удельной потенциальной энергии положения. Для идеальной жидкости сумма трех удельных энергий (полный напор) по длине элементарной струйки постоянна.

В общем уравнение Бернулли является специальным выражением основного физического закона сохранения энергии.