Сила давления жидкости на плоские стенки.

Рис.2.7.

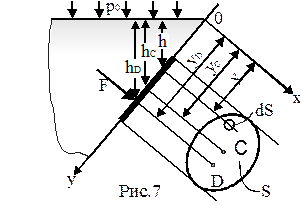
Используем основное уравнение гидростатики (2-11) для нахождения полной силы давления жидкости на плоскую стенку, наклоненную к горизонту под углом 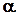(рис.2.7.). Рассмотрим участок стенки, ограниченный произвольными контуром и имеющий площадь равную S. Ось x направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось y перпендикулярно к этой линии в плоскости стенки. Выделим бесконечно малую площадку dS и выразим элементарную силу давления dF, приложенную к этой площадке:

;

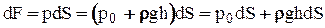где h - глубина, расположения площадки dS.

Для определения полной силы F проинтегрируем полученное выражение по всей площади S:

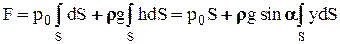
h=ysina из чертежа (рис. 2.7.); где y - координата площадки dS.

Интеграл 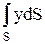представляет собой статический момент площади S относительно оси x и равен произведению этой площади на координату ее центра тяжести (т.С), т.е. .

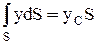Следовательно,

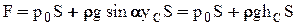
где 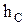- глубина расположения центра тяжести площади S

или

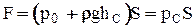(2-12)

Таким образом, полная сила давления жидкости на плоскую стенку равна произведению площади стенки на гидростатическое давление в центре тяжести этой площади.

В случае, когда 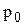является атмосферным и действует также с другой стороны стенки, сила F равна лишь силе давления от веса жидкости:

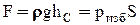(2-13)

Рассмотрим вопрос о точках приложения этих сил, называемых центрами давлений. Т.к. внешнее давление передается всем точкам площади одинаково, то и его равнодействующая будет приложена в центре тяжести площади. Для нахождения точки приложения силы гидростатического давления от веса жидкости (т. Д) применим теорему механики: момент равнодействующей силы относительно оси x равен сумме моментов составляющих сил

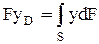где 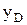- координата точки приложения силы F.

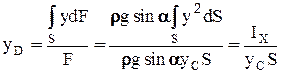
где 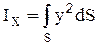- момент инерции площади S относительно оси x.

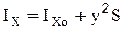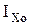Учитывая, что (где - момент инерции площади S относительно центральной оси, проходящей через центр тяжести и параллельной оси x), получим:

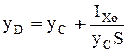(2-14)

Видно, что сила гидростатического давления приложена ниже центра тяжести фигуры на величину 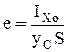, называемую эксцентриситетом давления (см. рис. 2.7., точки С и D).

Рис.2.8.

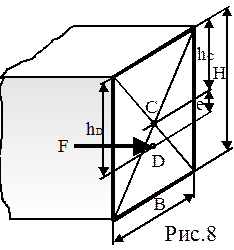
В качестве примера рассмотрим задачу (рис.2.8.) по определению силы гидростатического давления, действующей на плоский затвор высотой H=6м и шириной B=2м, который поддерживает жидкость в канале глубиной также H.

Величина силы:

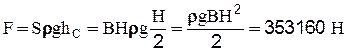
Глубина погружения центра давления:

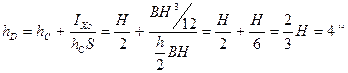
Момент инерции относительно центральной оси для прямоугольника:

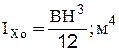
Таким образом, эксцентриситет давления составил:

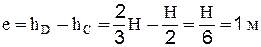
Иными словами, результирующая сила гидростатического давления, действующей на плоский затвор, величиной около 35 т, приложена не в центре тяжести (т.С), а в центре давления (т.D), который смещен вниз на e=1м относительно центра тяжести.