Основное уравнение гидростатики.

Рассмотрим наиболее важный для практики частный случай равновесия жидкости, находящейся под действием только сил тяжести. В этом случае проекции объемных (массовых) сил на оси будут равны:

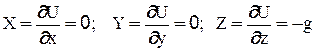
Следовательно, дифференциальное уравнение (2-9) примет следующий вид: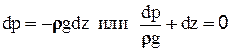

В результате интегрирования имеем: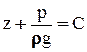

или при пограничных условиях 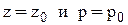имеем:

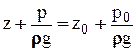(2-10)

где 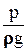- напор давления или пьезометрический напор;

z - нивелирная высота или расстояние которое отсчитывается от плоскости сравнения. (Плоскость сравнения выбирается произвольно, но эта плоскость должна быть горизонтальной).

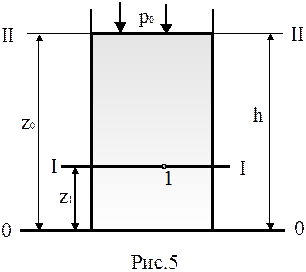
Видоизменим уравнение (2-10). Допустим, что нужно найти давление в т.1, погруженной на глубину h (рис.2.5.). Плоскость сравнения 0-0 проведем через днище резервуара. Плоскости I-I и II-II проведем через т.1 и свободную поверхность, соответственно. При давлении на свободной поверхности p₀ формула (2-10) примет вид:

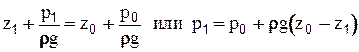
Видно, что 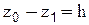и окончательно получаем:

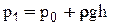(2-11)

Рис.2.5.

это уравнение является фундаментальным и называется основным уравнением гидростатики и показывает, что гидростатическое давление в любой точке покоящейся капельной жидкости изменяется в зависимости только от вертикальной координаты этой точки.

Величина 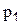в (2-11) называется абсолютным гидростатическим давлением в т.1. Оно равно абсолютному давлению на свободной поверхности 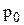плюс гидростатическое (или весовое) давление 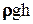, обусловленное весом самой жидкости.

Разность между абсолютным и атмосферным давлениями называется избыточным (манометрическим) давлением: .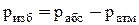

Если давление меньше атмосферного, то недостаток давления до атмосферного называют давлением вакуума:

.

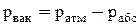Закон Паскаля.

Рис.2.6.

Согласно основному уравнению гидростатики (2-11) можно сделать вывод, что всякое увеличение внешнего давления 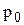увеличивает на такую же величину полное гидростатическое давление в любой точке жидкости.

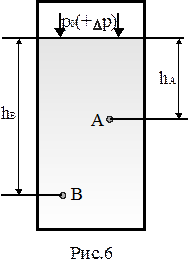
Давление в т. А и В (рис.2.6.) будут соответственно равны: 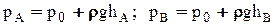. Изменив давление 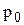на величину 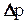, получим: 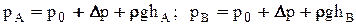, т.е. видно, что давление в т. А и В изменилось на одну и ту же величину. Таким образом внешнее давление, оказанное на свободную поверхность замкнутого объема несжимаемой жидкости, передается жидкостью одинаково всем ее точкам по всем направлениям - это закон Паскаля.